• data를 통해 우리의 믿음을 수정
  • data의 variance가 작고 믿음의 불확실성이 작은 곳에서는 decision이 쉽다.
    • ex> 주행 중에 신호등을 관찰하고 적색인지 녹색인지 판단
  • 반대로, data의 variance가 크거나 믿음의 불확실성이 큰 부분에서 수학이 도움이 된다.

2.1. Models of observations & models of beliefs

• 동전을 던져서 앞뒷면을 관찰하는 예제
  • model of observations
    • 매 flip시 bias가 같다/이전 flip 기억 못함
  • model of beliefs
    • coin이 공정할 것이나 어느정도는 bias될 수 있다.

2.1.1. Models have parameters

• 어떤 지역의 비가올 확률을 알고싶다.
  • input: 지역의 고도
  • output: 비가 올 확률
  • 이라하면 input으로 output을 도출해야하는데, 이 때 영향을 미치는 정도를 parameter라 한다.
• 동전 던지기 예제에서, 동전을 반으로 자르고 (뒷면의 무게-앞면의 무게)를 lopsidedness라고 해보자.
  • 
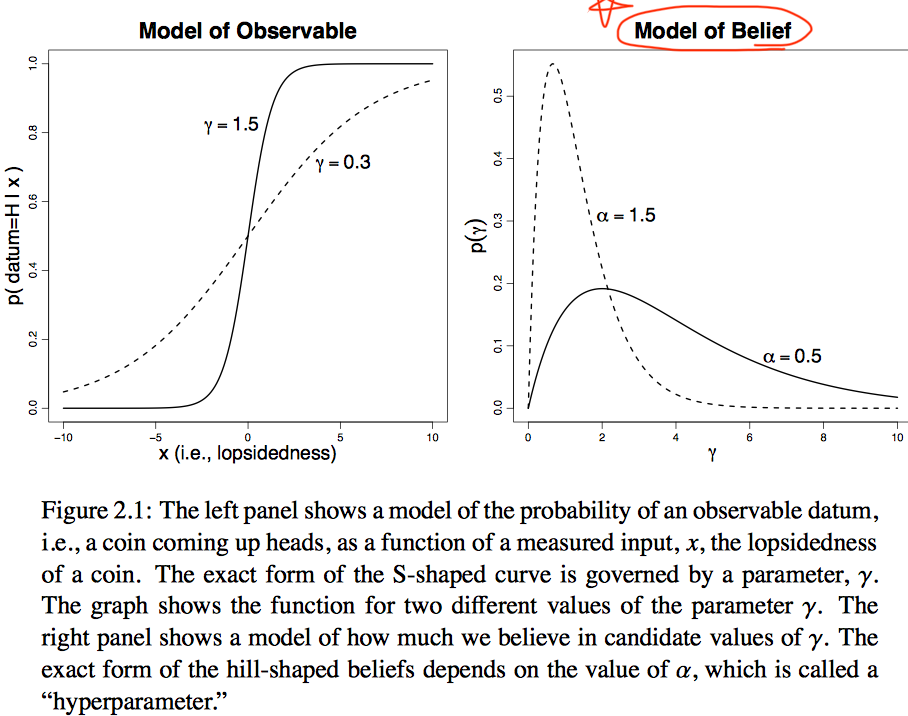
  • 동전의 기울기에 따라 앞면이 나올 확률이 달라진다고 모델링을 했는데, $\gamma$는 그 모델의 파라미터이다.
    • $p(\gamma)$:$\gamma$값의 candidate들을 얼마나 믿을 것인가에 대한 확률.
      • 여기서 $\alpha$는 hyperparameter이다.

2.1.2. Prior & posterior beliefs

• prior: 단순히 어떤 특정 data를 배제한 믿음
• posterior: data를 include한 믿음

2.2. Three goals for inference from data

• Estimation of parameter values
  • model과 데이터가 주어졌을 때, 가능한 parameter value들을 어느정도씩 믿어야하나?
• Prediction of data values
  • 현재 belief로 다른 data를 prediction
  • Bayesian inference에서는 믿음의 weighted average로 prediction이 된다.
• Model comparison
  • 모델이 여러개 있을 때, 하나씩 최적화해보고 좋은 모델 쓴다… 고얘기지 뭐…

2.3. R programming language -생략-