서론

계속 다루고 있는 확률 분포는 다음과 같은 성질을 가지고 있었다.

1. 상호 배타적인 two outcome.
2. stationary probability (어떤 outcome의 확률이 달라지지 않음)
3. data independent (순서에 따라 달라지지 않음)

Binomial에 대해서 어떤 prior belief들을 보기 시작할껀데… 먼저 likelihood function부터 정의해보도록하자

5.1 The likelihood function: Bernoulli distribution

• $p(y\vert \theta) = \theta^y(1-\theta)^{(1-y)}$
  • 위를 bernoulli distribution이라 한다.
  • y로 marginalize하면 1이 되지!
• 근데 y가 고정된 data고 $\theta$를 variable로 생각해볼 수 있다.
  • 이 경우 $\theta$의 likelihood function이라고 말할 수 있다.
  • 물론 이 경우 $\theta$의 확률과 연관은 되어있지만, pdf는 아니다.
    • $\int_0^1 \theta^y(1-\theta)^{(1-y)} d\theta = \frac{1}{2} \neq 1$
  • 이를 Bernoulli likelihood function이라 부른다.

5.2 A description of beliefs: The beta distribution

위에서 likelihood를 정의했는데, 당연히 $\theta$는 $[0, 1]$사이의 value이다. 우리가 prior를 정할 때 $p(\theta)$도 이 사이에서만 정의하면 된다. 이외에도 있으면 편리한 성질이 있는데

• $p(y\vert \theta)p(\theta)$ 가 $p(\theta)$꼴로 나오면 좋겠다.
  • 그러면 prior랑 posterior가 같은 함수 형태를 이룬다.
  • 데이터가 연속적으로 나와도 계속 같은 형태를 유지..
• $\int p(y\vert \theta)p(\theta)d\theta$가 analytically 풀리기를 기대함
  • $p(\theta)$가 $p(y\vert \theta)$의 conjugate prior !!!!
    • $p(y\vert \theta)$가 주어질 때, $p(\theta)$로 posterior를 만들 수 있고
    • 이 posterior가 prior와 같은 꼴일 때

이제 Bernoulli likelihood의 conjugate prior를 찾아보자! $\theta^a(1-\theta)^b$ 꼴 일테지..

그래서 Beta distribution이 conjugate prior인데…

$p(\theta\vert a,b) = beta(\theta;a,b) = \theta^{(a-1)}(1-\theta)^{(b-1)}/B(a, b)$

• $B(a,b)$: Beta function (normalizing term)
  • $\int_0^1 \theta^{(a-1)}(1-\theta)^{(b-1)} d\theta$
  • TODO: Gamma function 찾아보기( $B(a, b) = \Gamma(a)\Gamma(b)/\Gamma(a+b)$라고 한다. )
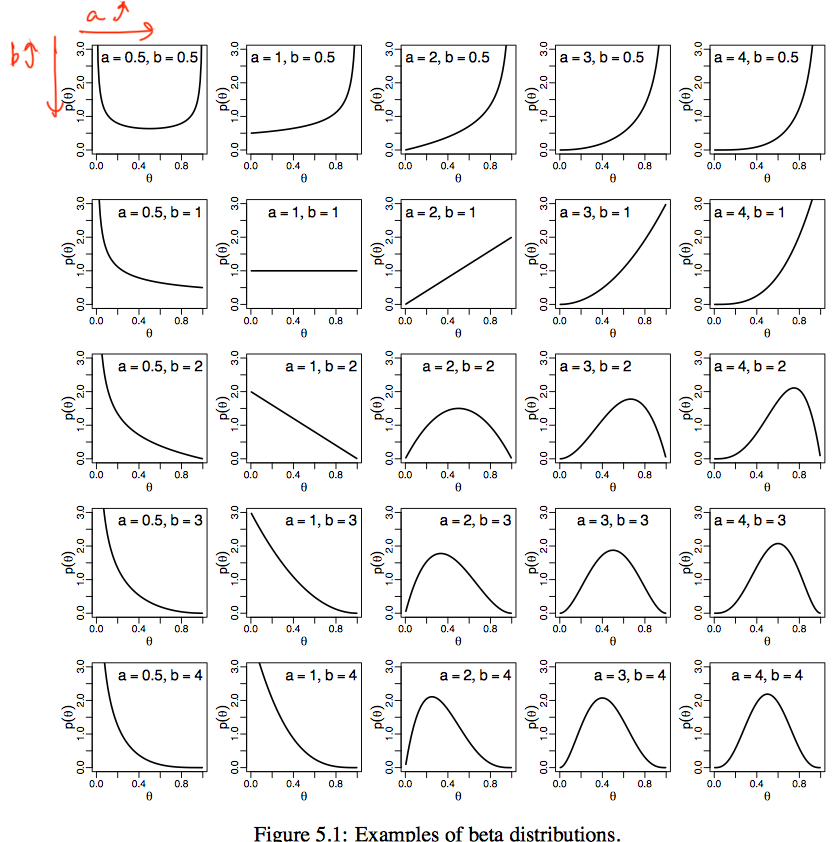
• a, b가 positive
• a가 커지면 오른쪽으로 이동, b가 커지면 왼쪽
  • 
• mean: $\mu = \frac{a}{a+b}$
  • a » b 면 mean 커짐
• std: $\sqrt{\mu(1-\mu)/(a+b+1)}$
  • a+b가 커지면 std 작아짐
• 그림의 대각선은 fair한 동전이다. a=b=1은 uniform dist, 4면 gaussian과 비슷하넹..
  • 이는 1번만 보면 fair할 것 같으나 확신이 부족한 것, 4번씩 번갈아 observe하면 확신이 생겼다고 볼 수 있지…

    prior 설정 시에, a, b >= 1을 많이 쓴다. 그림의 대각선을 보면 fairness에 관한 믿음으로 쓸 수 있겠지….

5.2.2 The Posterior beta

이제 beta distribution을 사용하여 posterior를 구해보면

• (1)에서 (2)가 되는 것은 beta dist의 정의에 따라 Normlize하면 당연히 그리 된다.
• 결론: $beta(\theta; a,b)$를 prior로 하여 data가 N개중 z개 head 나온 seq라면 posterior는 $beta(\theta; a+z, b + N - z)$이다.
• 다른 해석
  • mean을 구해보자
    • prior:
      • $$\frac{a}{a+b}$$
    • posterior:
      • $$\frac{a+z}{a+N+b} = \frac{z}{N}\frac{N}{N+a+b} + \frac{a}{a+b}\frac{a+b}{N+a+b}$$
      • 여기서 $z/N$은 data의 mean, $a/(a+b)$는 prior의 mean이며 이들의 weighted sum으로 볼 수 있다.

N번 돌리는데 왜 likelihood는 combination안하는가…?는 하나의 sequence가 observe 되었다고 가정하고 풀고있기 때문이다.

5.3 Three inferential goals

5.3.1 Estimating the binomial proportion

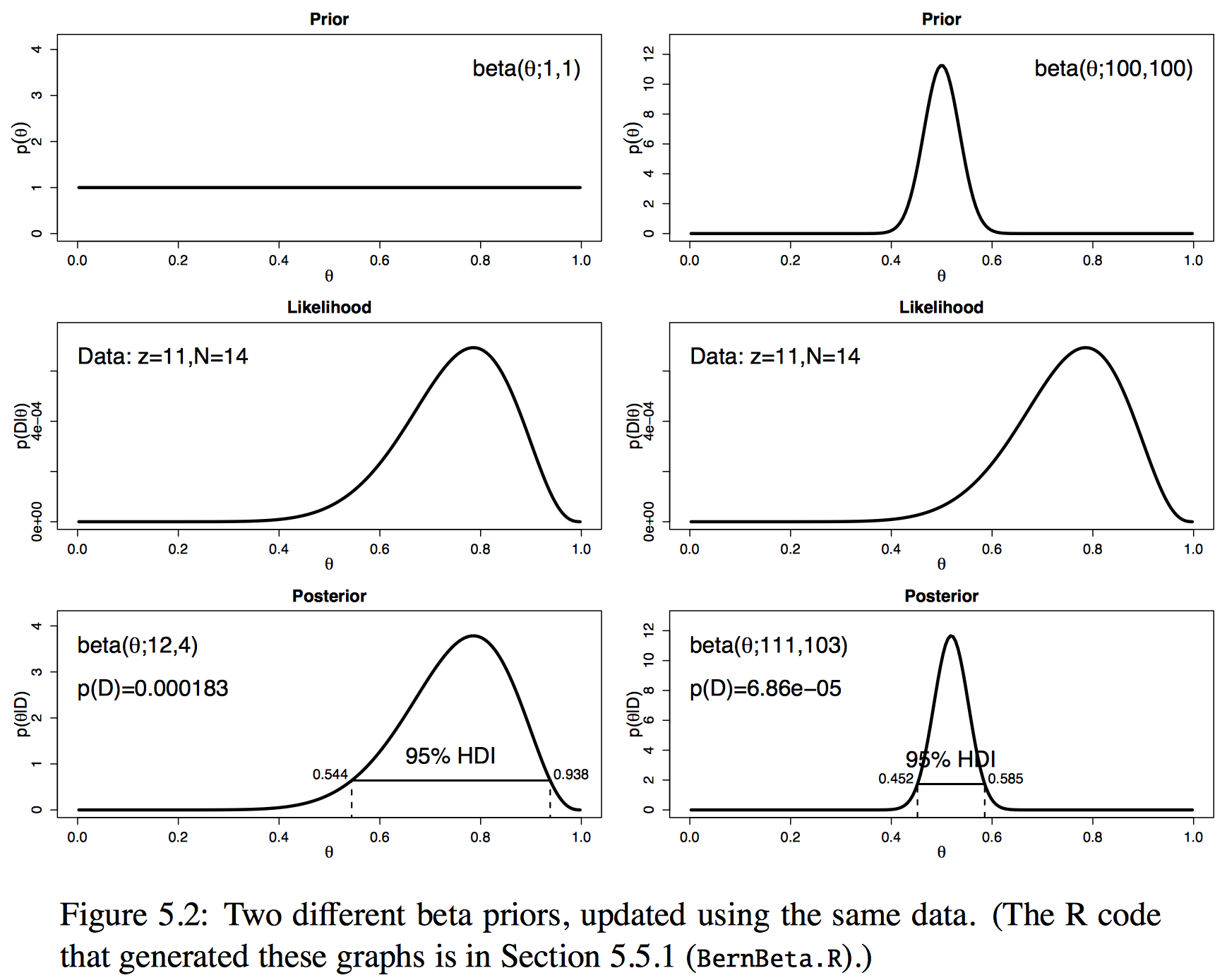
• prior의 belief 정도에 따라 posterior가 어떻게 바뀌나 보자..

5.3.2 Predicting data

• $p(y) = \int p(y\vert \theta)p(\theta) d\theta$로 모든 param의 belief들의 weighted sum으로 prediction이 가능하다고 했었다.
  • 요기서 $p(\theta)$가 observed data로 수정된 posterior belief…
  • $$\begin{align*} p(y=1) &= \int p(y=1\vert \theta) p(\theta\vert z, N) d\theta \\ &= \int \theta p(\theta\vert z, N) dθ \\ &= \frac{z + a}{N + a + b} \end{align*}$$
  • 뭐 수식이 필요친 않고.. Observed data로 수정된 belief를 가지고, weighted sum한 것이 prediction이다.

5.3.3 Model comparison

Evidence

어떤 모델의 evidence라는건 Data가 주어졌을 때, 모델의 가능성?을 보여주는 척도

• model과 data given -> 가능한 param에 대한 weighted sum
• $p(D\vert M) = \int p(D\vert \theta, M)p(\theta\vert M)d\theta$

여기서 $p(D\vert M)$은 prior를 beta, likelihood를 bernoulli로 하면 $p(z,N)$과 같다.

증명> $\begin{align*} p(D\vert M) &= \int p(D\vert \theta, M)p(\theta\vert M)d\theta \\ &= \int \theta^z(1-\theta)^{(N-z)}\cdot\theta^{a-1}(1-\theta)^{b-1}/B(a,b) d\theta \\ &= \int \theta^z(1-\theta)^{(N-z)}\theta^{a-1}(1-\theta)^{b-1}/[B(a,b)\cdot p(z,N)] \cdot p(z,N) d\theta \\ &= \int beta(\theta; a+z, N-z+b) \cdot p(z,N) d\theta \\ &= p(z,N) \int beta(\theta; a+z, N-z+b) d\theta \end{align*}$

엄청 헷갈리네… ㅠㅠ

어쨌든 여기서 $p(z,N)$이 evidence임을 증명했고…

이를 구해보면 (1),(2)에서 $B(a, b)p(z,N) = B(z+a, N-z+b)$ $p(z,N) = B(z+a, N-z+b)/B(a, b)$

Beta function으로 data의 prior를 표현가능하다??

hyperparameter (a, b)는 사실 필요하지! $p(z,N\vert a,b)$

그림 재탕 위의 그림에서 P(D)는 사실 P(D\vert M)인데 Data에 따른 evidence가 왼쪽이 훨씬 큰 것을 알 수 있다.