Hulk의 개인 공부용 블로그

ch 7. Inferring a Binomial Proportion via the Metropolis Algorithm

30 Oct 2017 | ml bayesian inference mcmc

호객행위

d3를 가지고 만들어본 예제이다. 왼쪽이 실제 distribution이며, 오른쪽이 sampling을 한 결과이며, burn-in은 따로 하지 않았다.

population

markov-chain

sampled

Intro

  • 우리가 원하는건 posterior $p(\theta \vert D)$
  • 근데 항상 evidence가 marginalize하기 쉽지 않다.
    • Ch 5에서는 likelihood의 conjugate prior를 찾아서 posterior를 구했음
    • Ch 6는 그냥 prior를 discrete하게 쪼개놓고 구했음 (굳이 정리를 하지 않았음)
      • 잘게 쪼개면 더 정확해진다
  • Ch 6는 좋은 방법이지만 parameter가 많아지면 어떡할랭?
    • 1000개씩 6개의 파라미터면 $1000^6$이 돼버림..
  • posterior와 비례하는 어떤 함수를 가지고있고, 계산할 수 있으면
  • 많은 수의 random value들로 시뮬레이션해서 posterior distribution을 근사시켜보자!

Metropolis algorithm

예제

  • 정치인이 여러 섬들을 다니면서 유세를 할 것이다.
  • 섬은 총 7개가 있으며, 각 섬마다 인구 수는 다르다.
  • 정치인은
    • 현재 섬에 머무를지,
    • 서쪽 섬으로 갈지,
    • 동쪽 섬으로 갈지 판단해야한다.
  • 지금 섬의 인구와, 다음에 갈 섬으로 제안된 곳의 인구 수만 알 수있다.

algorithm

  • proposal distribution
    • 동전을 던져 왼쪽으로 갈지, 오른쪽으로 갈지 정한다
  • 한쪽이 나왔다면
    • 한 쪽의 인구수가 더 많으면 무조건 이동
    • 아니라면 $P_{move} = P_{proposed} / P_{current}$의 확률로 감

근데 이게 먹힌다.

결과

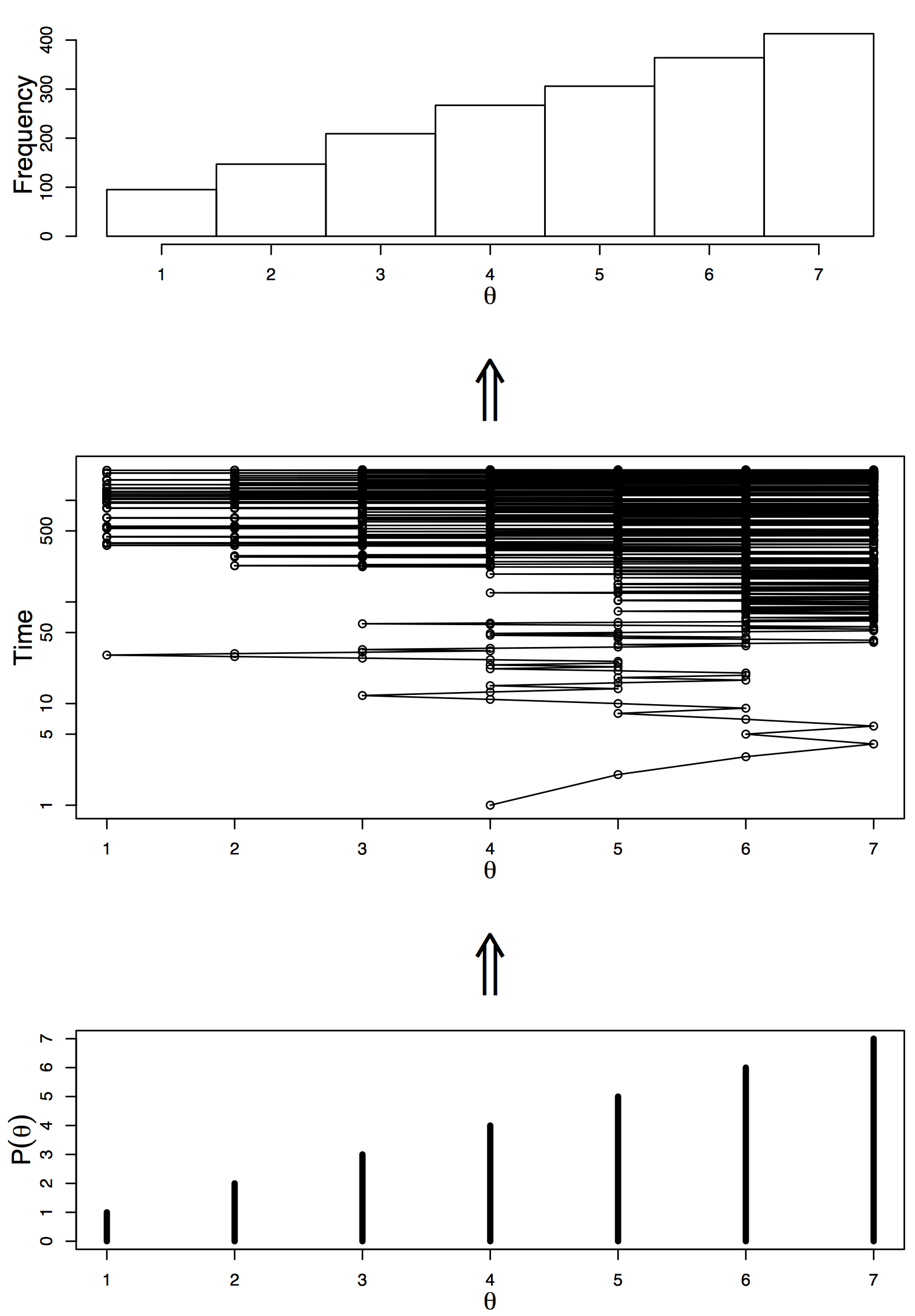
MA.png

알아야할 것들

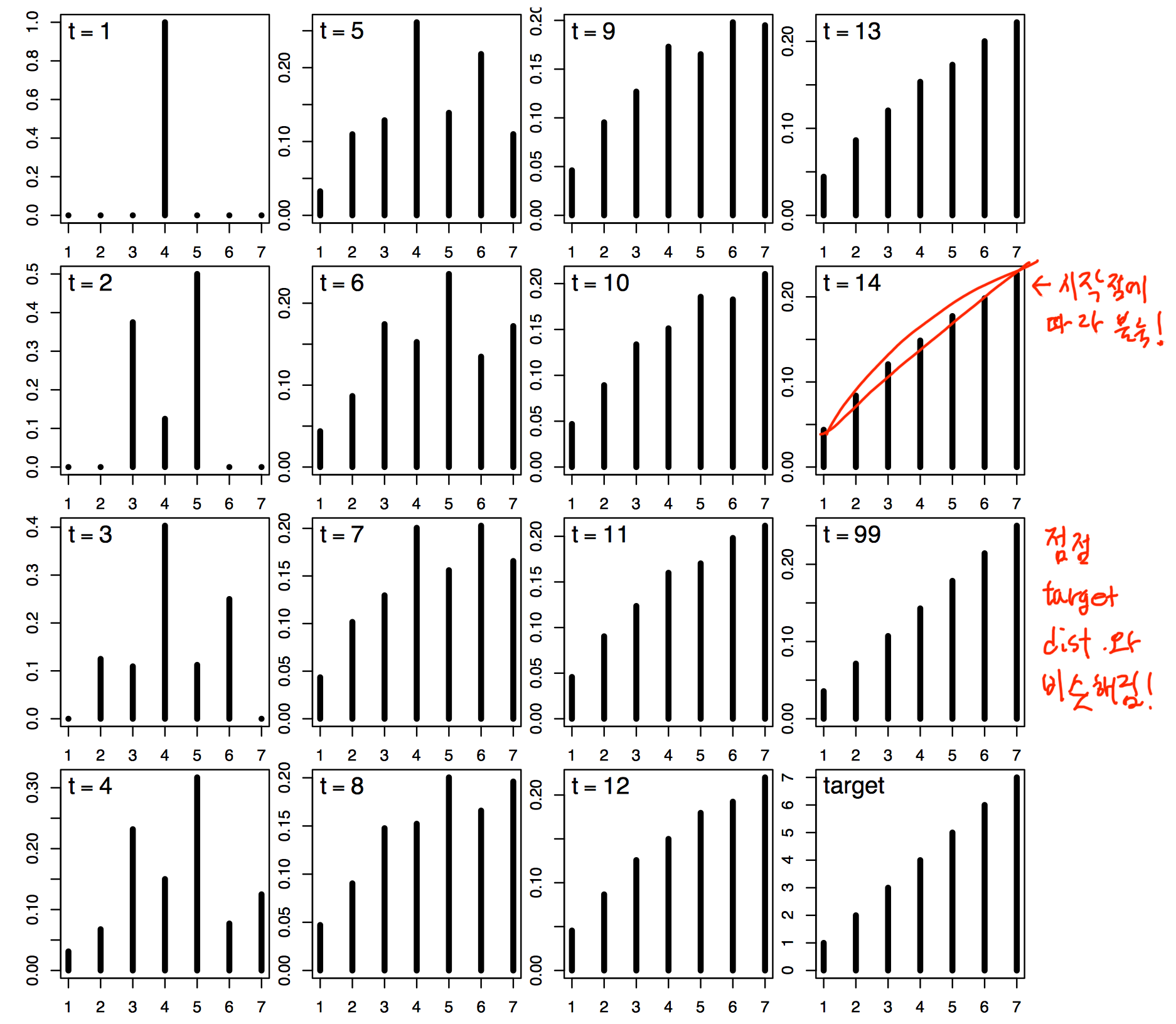
MA2.png

  • burn-in
    • 앞의 몇 스텝은 초기값에 따른 bias가 있으니 없앰
  • proposal distribution을 잘 선택해야함
    • narrow하면 수렴에 엄청 오래걸릴 것이다
    • 초기값이 심지어 target distribution이 flat하고 low한 곳이면 수렴이 힘들지..

근데 이게 여태 하던 posterior 추정이랑 뭔 상관?

  • Metropolis algorithm을 다시 한번 보면
    • 이동할 확률을 $\frac{P_{proposed}}{P_{current}}$로 구함
    • 즉 $P$가 normalized돼있지 않아도 됨!
      • $P = p(D\vert \theta)p(\theta)$로도 충분
    • 그래서 posterior를 추정할 때 좋지!

코드로 풀어보자!

동전던지기의 예제를 들어본다. $\theta$는 앞면이 나올 확률을 의미하는 parameter이다.

가정

  • Prior
    • $p(\theta): uniform(0,1)$
  • Likelihood
    • $p(z,N\vert \theta): \theta^{z}(1-\theta)^{(N-a)}$
  • data
    • 14번 던져서 11번이 앞면이 나옴.

Proposal distribution

$N(0, 0.2)$로 하며, 부적절한 $\theta$에 대해서는 prior나 likelihood가 0을 주면 된다.

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt

def prior(theta):
    '''
    theta에 대한 prior 확률을 return
    '''
    if theta < 0 or theta > 1:  # 여기서 처리해주자!
        return 0
    else:
        return 1

def likelihood(z, N, theta):
    '''
    theta가 주어졌을 때, z,N에 대해서 likelihood 확률을 return
    '''
    return (theta ** z)*((1-theta)**(N-z))

def proposal_dist(n):
    '''
    proposal distribution에서 n개 뽑아온다.
    '''
    return np.random.randn(n) * 0.2  # sigma는 0.2로...

N = 10000
burn_in = int(0.1*N)
theta_sampled = [0.5]

for i in range(N):
    theta = theta_sampled[-1]
    new_sample = proposal_dist(1)    
    proposed_theta = theta + new_sample
    
    # p(D\vert ∂)p(∂) 구하기
    h1 = prior(theta) * likelihood(11, 14, theta)
    h2 = prior(proposed_theta) * likelihood(11, 14, proposed_theta)
    
    if h2 > h1:  # 만약 proposed가 더 확률이 크면
        theta_sampled.append(proposed_theta)
    else:  # 아니면
        s = np.random.uniform(0, 1, 1)
        if s[0] < h2/h1:
            theta_sampled.append(proposed_theta)
        else:
            theta_sampled.append(theta)


theta_sampled = theta_sampled[burn_in:]  # 처음 나온 애들은 버려야지..
plt.hist(np.array(theta_sampled), bins=50)
plt.show()

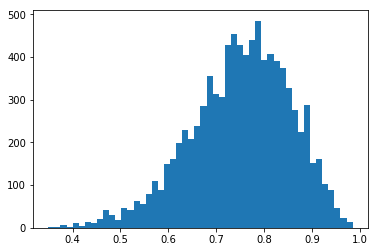Unknown.png 결과를 보면 잘 나오는 것을 알 수 있다.

Related Posts