2 Binomial이 독립인 사건에 대해서 analytic하게 풀기

• $\theta_1, \theta_2$가 각각 다른 동전이 앞면이 나올 확률을 의미한다고 가정해보자.
• 그렇다면 likelihood는 다음처럼 정의된다.
  • $p(D\vert \theta_1, \theta_2) = \theta_1^{z_1}(1-\theta_1)^{(N_1-z_1)}\cdot\theta_2^{z_2}(1-\theta_2)^{(N_2-z_2)}$
• 또한 posterior는
• $p(\theta_1, \theta_2 \vert D) = p(D\vert \theta_1, \theta_2)p(\theta_1, \theta_2)/ \left [ \int\int p(D\vert \theta_1, \theta_2)p(\theta_1, \theta_2)d\theta_1d\theta_2 \right ]$
  • 요기서 두 $\theta$가 독립이라고 하면 ch 5에서 본 beta distibution을 사용해서 또 analytic하게 풀 수 있다.
• $$\begin{align*} p(\theta_1, \theta_2 \vert D) &= p(D\vert \theta_1, \theta_2)p(\theta_1, \theta_2)/ p(D) \\ &= \frac{\theta_1^{z_1+a_1-1}(1-\theta_1)^{(N_1-z_1+b_1-1)}\cdot\theta_2^{z_2+a_2-1}(1-\theta_2)^{(N_2-z_2+b_2-1)}}{p(D)\cdot B(a_1,b_1)\cdot B(a_2,b_2)} \end{align*}$$
• 정리하면 $p(D) = \frac{B(z_1+a_1, N_1-z_1+b_1)\cdot B(z_2+a_2, N_2-z_2+b_2)}{B(a_1,b_1)\cdot B(a_2,b_2)}$ 가 나온다.

approximation -> Gibbs

• parameter space가 작을 때는 grid approximation이 좋은 대안이다.
  • 어떤 prior distribution도 쓸 수 있다.
  • 어떤 posterior에서 HDI 구할 때도 편하다.
• 하지만 parameter가 넓을 경우는 힘들어진다.
  • 그럼 7장의 Metropolis algorithm을 쓰면?
  • proposal dist.의 디자인에 따라서 local region에 계속 머물수도 있다.
• Gibbs sampling을 소개해보자

Gibbs sampling

• proposal distribution같은거 없음!
• 대신 나머지 파라미터가 주어진 posterior dist.에서 sampling이 가능해야함(더 빡셈)
  • 즉 $\theta_1, \theta_2, \theta_3$이 parameter라고 하면
    • $p(\theta_1\vert \theta_2, \theta_3, D)$
    • $p(\theta_2\vert \theta_1, \theta_3, D)$
    • $p(\theta_3\vert \theta_1, \theta_2, D)$
  • 에서 모두 sampling이 가능해야함.
• 엄청 빡센데, 요건만 만족하면 Metropolis algorithm보다 훨씬 reliable하다.
• 이 놈 역시 MCMC process
  • 현재 position에서만 다음 스텝이 결정되고,
  • sampling을 통해 simulation하니까
• 보통은 순서를 정해서 파라미터를 순회하면서 sample한다.
  • parameter가 많아지면 random하게 파라미터를 뽑을 시, 다 뽑는데 시간이 걸림
• Gibbs sampling은 Metropolis에서 proposal distribution이 지금 뽑을 parameter에 의존하는 것이라고 볼 수 있다고 한다. (이 부분 좀 잘 모르겠다..)
  • 이 경우 proposal distribution이 항상 그 파라미터의 posterior probability를 반영해서, proposal이 항상 accept된다.

여기까지 보고 다시 위의 2 Binomial 예제를 Gibbs sampling으로 풀어보자!

사실 위의 예제는 너무 단순하긴한데… 그대신 쉬우니까…

• $\theta_1$에 대한 posterior는
  • $$\begin{align*} p(\theta_1\vert \theta_2, D) &= p(\theta_1\vert D) \\ &= beta(\theta_1\vert z_1+a_1, N_1-z_1+b_1) \end{align*}$$
• 요걸 가지고 실험을 해보자!

Gibbs Sampling 예제

동전던지기의 예제를 들어본다. $\theta_n$은 n번째 동전이 앞면이 나올 확률을 의미하는 parameter이며, 동전은 2개이다.

가정

• Prior
  • $p(\theta_n): beta(\theta \vert 3,3)$
• Likelihood
  • $p(z_n,N_n \vert \theta_n): {\theta_n}^{z_n}(1-{\theta_n})^{(N_n-z_n)}$
• data
  • 동전 1 - 7번 던져서 5번 앞면
  • 동전 2 - 7번 던져서 2번 앞면

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

data = [{'N': 7, 'z': 5},
        {'N': 7, 'z': 2}]

def posterior(N, z, a, b):
    return np.random.beta(z + a,
                          N - z + b)
thetas = [[0.2, 0.5]]
for i in range(100000):
    idx = i % 2
    theta = thetas[-1].copy()
    theta[idx] = posterior(data[idx]['N'],
                           data[idx]['z'],
                           3,
                           3)  # prior가 좀 세다. 1로 바꾸면 좀 더 data와 비슷하게 나옴을 알 수있다.
    thetas.append(theta)

thetas = thetas[int(len(thetas)*0.1):]  #burn-in
    

np_thetas = np.array(thetas)
x = np_thetas[:,0]
y = np_thetas[:,1]
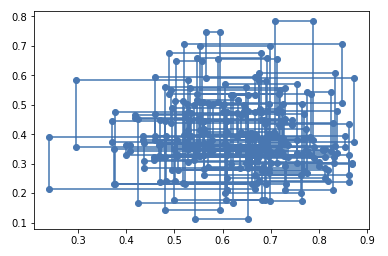
plt.plot(x[:300], y[:300], '-o')
plt.show()

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

hist, xedges, yedges = np.histogram2d(x, y, bins=20, range=[[0, 1], [0, 1]])

xedges, yedges = np.meshgrid(xedges, yedges)

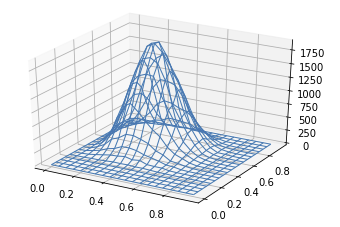
surf = ax.plot_wireframe(xedges[:-1,:-1],
                         yedges[:-1,:-1],
                         hist,
                         linewidth=1)

Gibbs sampling의 단점

• 각 파라미터의 conditional probability가 필요!
• 연관도가 높은 파라미터들에 대해서 progress가 멈출 수 있음
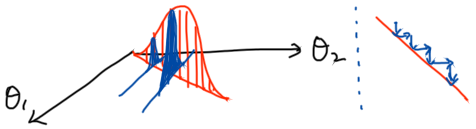  • $\theta_1$과 $\theta_2$가 Highly correlated 면 왼쪽과 같은 그림이 되겠다. 이 때, 파라미터 업데이트는 오른쪽처럼 아주 작게 움직이겠다.