Gaussian Process

Supervised learning 타입

Supervised learning을 두 가지 타입으로 나눠볼 수 있다.

• 고려할 함수들의 class를 제한하는 방법(예> linear function with some degree)
  • 함수의 richness를 잘 살려야 함
    • 너무 rich하게 잡으면 overfitting
    • 너무 작게 잡아버리면 poor prediction.
• 모든 가능한 함수의 prior probability를 주는 방법
  • 이 쪽이 Gaussian process

Bayesian linear model

아주 쉬운 예제로 Linear model이 다음처럼 있다고 가정하자.

where $\epsilon \sim N(0, \sigma_n^2)$

• w의 prior distribution을 가정(Bayesian…)
  • $\textbf{w} \sim N(\textbf{0}, \Sigma_p)$
• likelihood
  • $p(\textbf{y}\vert \textbf{X}, \textbf{w}) = N(\textbf{X}^T\textbf{w}, \sigma_n^2I)$
• posterior
  • $p(\textbf{w}\vert \textbf{X},\textbf{y}) \sim N(\frac{1}{\sigma_n^2}A^{-1}\textbf{X}\textbf{y},\ A^{-1})$
  • $A=\sigma_n^{-2}XX^T+\Sigma_p^{-1}$
• prediction
  • $$p(f_*\vert \textbf{x}_*, \textbf{X}, \textbf{y}) = \int p(f_*\vert \textbf{x}_*, \textbf{w}) p(\textbf{w}\vert \textbf{X}, \textbf{y}) d\textbf{w}$$

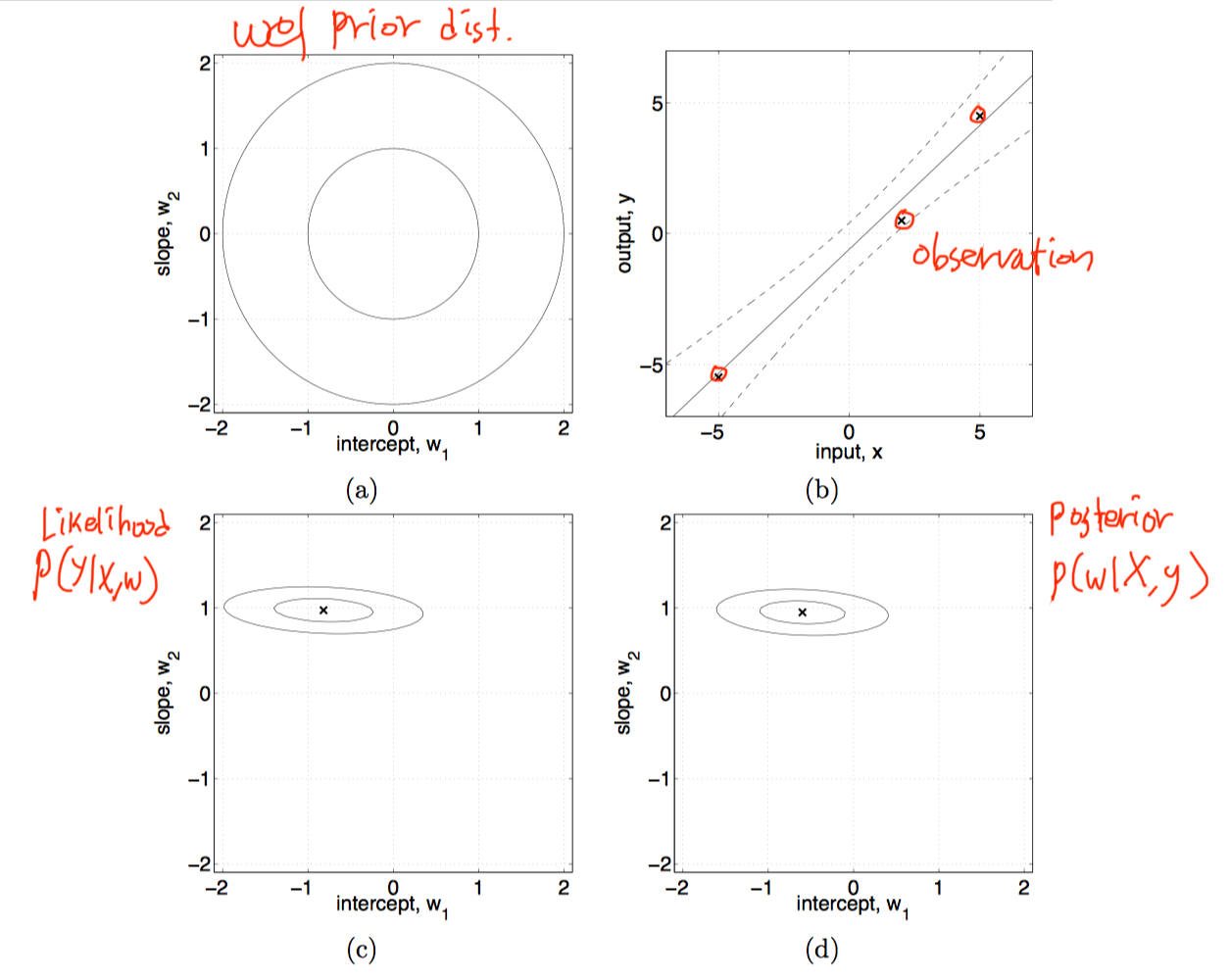Observation에 의해서 posterior를 구할 수 있었으며, 위의 prediction 식을 사용하여 새로운 y값을 구할 수 있다. 이제 linear model이 아닌 kernel trick을 쓰면 Gaussian process!