참고1 참고2 pytorch 코드

Variational autoencoder

• $p(x, z) = p(x\vert z)p(z)$
  • $x$: data
  • $z$: latent variable

Generation process

• 각 datapoint i에 대해
  1. $z_i \sim p(z)$를 draw한다.
  2. $x_i \sim p(x\vert z)$를 draw한다.

위 과정을 graphical model로 표시하면 다음 그림과 같다.

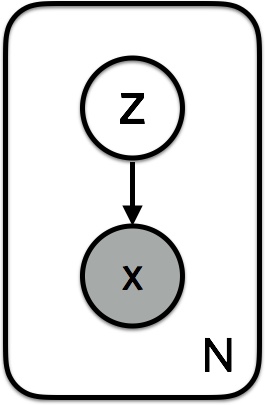
Goal of objective

우리가 원하는 것은 데이터가 주어졌을 때, 이를 가장 잘 표현하는 z를 찾고싶은 것!

• 여기서 $p(x)=∫p(x∣z)p(z)dz$ 인데 이를 구하기 힘듬!
• 그래서 posterior를 근사시킬 필요가 있으며,
• Variational inference는 posterior를 어떤 distribution family들 $q_\lambda(z\vert x)$로 근사시킨다.
  • $q_\lambda(z\vert x)$가 $p(z \vert x)$와 유사하도록 $\lambda$ 값을 찾아나간다.
  • 
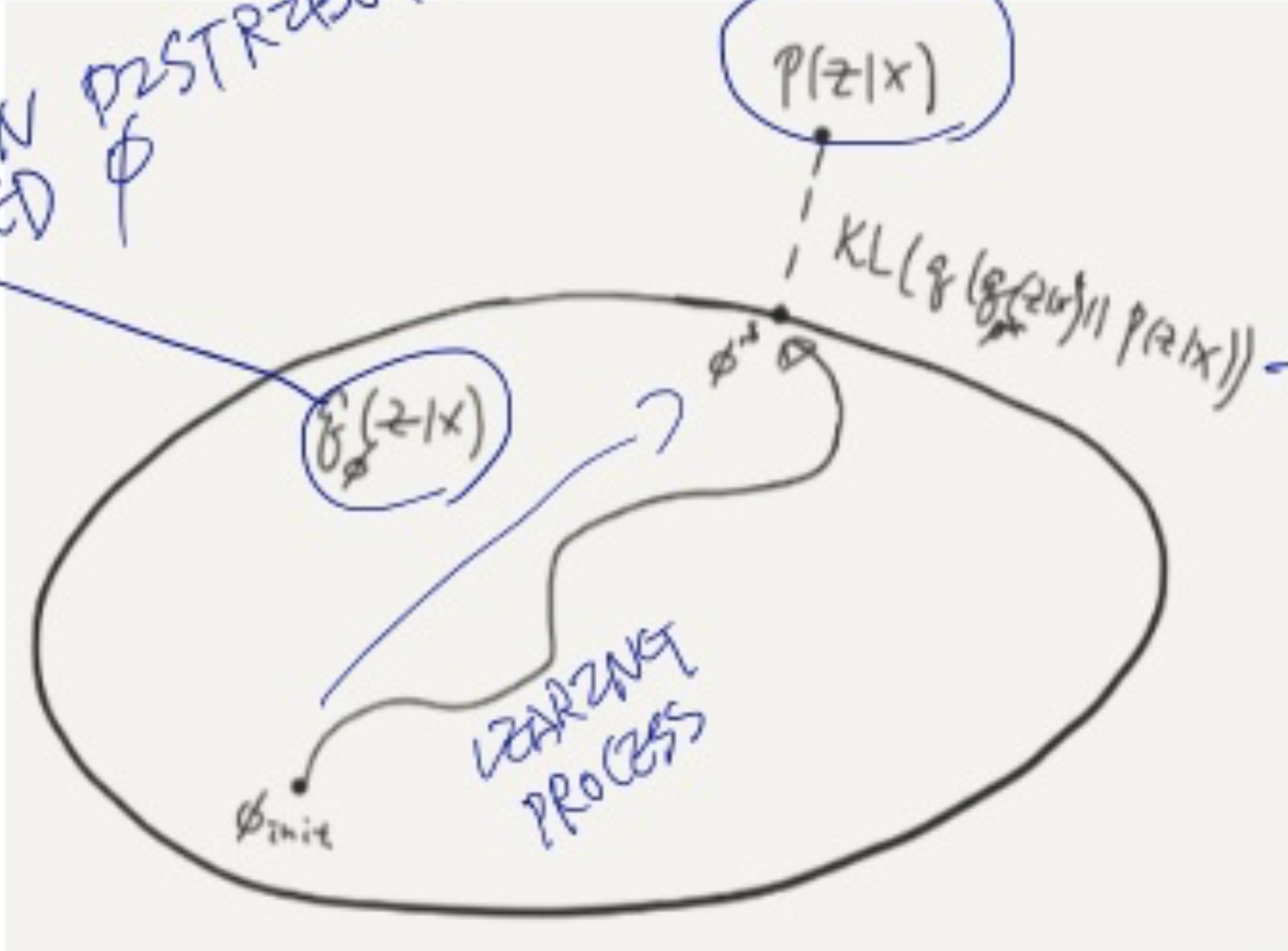
• 유사한 값을 찾기위해 KL-divergence를 쓰고, 정리해보면 다음처럼 나온다.
  • $$KL(q_\lambda(z \vert x) \vert\vert p(z\vert x)) = logp(x)-\left ( E_q[log{p(x\vert z)}] - KL(q_\lambda(z\vert x) \vert\vert p(z)) \right ) -- (1)$$
  • 그래서 $KL(q_\lambda(z\vert x) \vert\vert p(z\vert x))$를 minimize하는 것은
  • $E_{q_\lambda(z\vert x)}[log( p(x\vert z) )] - KL(q_\lambda(z\vert x) \vert\vert p(z))$ 를 maximize하는 것!
    • $p(x\vert z)$가 decoder
    • $q_\lambda(z\vert x)$를 encoder
    • 로 만들어버린 뒤 위 식을 maximize, 즉 위 식에 -를 곱한 값을 loss function으로 하고 학습시키면 VAE 완성

(1) 식 유도.. 증명의 맨 첫줄의 x,z는 X,Z이다. (전체 셋을 의미함)