Hulk의 개인 공부용 블로그

GAN

02 Nov 2017 | ml generative model

참고 1

생김새

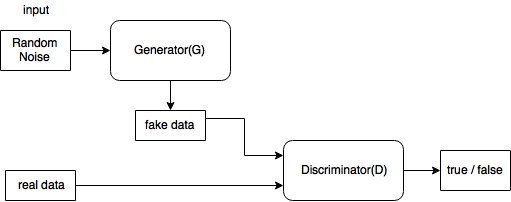GAN.png 요래 생겼다.

푸는 문제

where

D 관점에서 (1)의 앞 뒤의 수식을 따로 생각해보면

    • data에서 나온 x(real data)는 값을 크게하고
    • $p_z$를 통해 나온 $z$가 Generator를 거쳐 나온 G(z)(fake data)는 값을 작게해야

V(D, G)를 크게할 수 있다.

이제 G 관점에서 (1)의 뒷 수식만 보면

    • 이걸 minimize하려면 $G(z)$가 최대한 x의 분포에 가깝게 가야한다.

논문에 있는 그림인데,

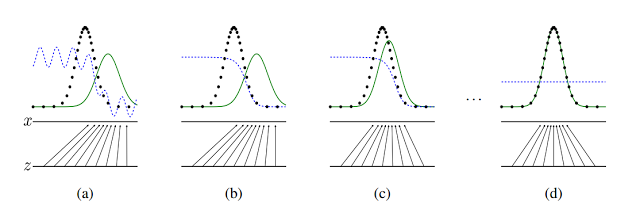
  • 검은색: data distribution
  • 초록색: generator distribution
  • 파란색: discrimimnator distribution

실용적인 수식 변환

사실 (1)에서 $log(1-D(G(z)))$를 minimize하는 대신 $log(D(G(z)))$를 maximize 한다. 처음에 G가 너무 구려서 Discriminator가 구분을 잘함. 그래서 $log(1-D(G(z)))$에 대한 gradient가 0에 가까움.. 근데 $log(D(G(z)))$는 괜찮음.

이론

제안 1.

G가 고정되어있으면 최적의 discriminator D는

증명 >

  1. 일단 이것부터 증명하자. $\forall (a, b) \in \textbf{R}^2 - {(0, 0)}$에 대해 어떤 함수 $y \rightarrow a\cdot log(y) + b\cdot log(1-y)$가 존재한다면 [0, 1]사이에서 f(y)가 최대가 되는 y는 $\frac{a}{a+b}$.

미분해서 0이되는 y를 찾으면 당연히 저 값이 나온다. 로그 두개를 하나는 반대로 만들어서 더한 꼴인데, 볼록한 형태일테고… 쉬우니까 넘어가자.

1을 증명했으면 이제 $V(D,G)$를 전개해보자

인데 제안 1을 사용하면 증명 끝이지?

위의 제안으로부터 $ \underset{ D}{max} V(D, G) $는 다음처럼 바뀐다.

Thorem 1.

$C(G)$의 global minimum이 달성 <=> $p_g = p_{data}$. 그리고 그 때 $C(G)$의 값은 $-log(4)$

증명>

  1. $p_g = p_{data}$일 때 C(G)값 증명

$p_g = p_{data}$면 $D^*_G(x)=\frac{1}{2}$는 당연하고.. 이를 $C(G)$에 넣어보면

  1. (<=>)증명 이제 KL이나 JSD가 >=0 이니까 최저값은 -log(4)이고 그 때 $p_{data} = p_g$

두번째서 세번째 넘어가는것만 보이자

이제 남은 건 G, D가 충분한 capacity일 때 GAN 알고리즘이 $p_g = p_{data}$를 achieve 하는가 증명인데…. 이건 패스

Related Posts