Hulk의 개인 공부용 블로그

BEGAN

15 Nov 2017 | ml generative model

참조(여기는 v1논문, 내가 본건 v4논문… condition이 좀 많이 다르다.)

W-distance 설명!! 요걸 기반으로 좀 더 공부해야할 듯..함!

W-gan의 세줄다섯줄 요약!

  • distance metric을 통해 probability를 최소화시키고싶음
  • KL-divergence를 보통 썼는데… 얘는 불연속에 불편함이 많아서 w_dist를 써보자!
  • 얘는 1-lipschitz함수로 sup을 찾는것과 같다.
  • 그래서 $\theta$ 그대로 놓고 f를 업데이트하고(여러번) 그 f로 $\theta$ 업데이트
  • Improving W-gan에서는 이것자체도 loss에 넣어버림

Introduction

  • GAN의 단점
    • 학습이 어려움
      • Hyper parameter 잘골라야…
      • training을 위한 trick도 많아…
      • D, G사이의 밸런스도 맞추기 힘들어…
    • Model collapse
      • discriminator를 속이는 한 예제만 죽어라 파는 것..
  • 이 논문의 contribution
    • 간단하고, 강인한 구조로 빠르고 stable한 수렴을 이룸
    • Discriminator와 Generator간의 밸런스를 맞추는 equilibrium concept를 제안함 -> $\gamma$
      • image의 diversity와 quality간의 trade-off를 조정하는 방법을 제시
    • convergence에 대한 approximate measure를 제안함.

Related Work

  • DCGAN - CNN으로 트레이닝하는 방법을 제안
  • EBGAN - Discriminator를 AutoEncoder(AE)로 제안(사실 Energy based라는데… 그냥 AE가 맞는 듯)
  • WGAN - JSD->wasserstein dist로 바꿔서 구현 간소화
    • 사실 잘 모르겠다…

Proposed Method(Equilibrium 없이..)

먼저 Equilibrium이 없이 설명한다. 이 이후에 나오니까 걱정 ㄴㄴ

  • 기존 GAN은 sample들의 distribution이 잘 matching되도록 트레이닝
  • 이를 sample들의 AE-loss의 distribution을 matching하도록 바꿈
  • 그리고는 이 loss의 Wasserstein distance의 lower bound를 계산하고,
  • 이를 최대화하는 것이 D의 역할
  • 반대가 G의 역할

AE-loss 정의

  • $ \cal{L}:\mathbb{R}^{N_x}\mapsto \mathbb{R}^+ $
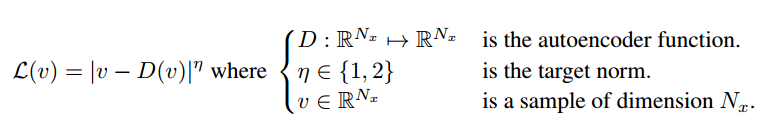  • AE-loss.png 그냥 단순히 AE를 거친 input과 output의 pixel별 로스를 구해서 l-1,l-2 norm중에 하나를 취한다.

W-distance

먼저 $\mu_1$을 real-image에서의 AE-loss의 distribution, $\mu_2$를 generation한 image의 AE-loss의 distribution이라 하자.

  • $\Gamma(\mu_1, \mu2)$: marginal distribution이 $\mu_1, \mu2$인 모든 joint distribution. (어떤 녀석인지 직감적으로 안와닿는다.. 다음 섹션 참조!)

위 수식이 W-distance라는데 먼저 $\gamma$에 대해서 생각해보자.

  • $\gamma(x_1, x_2) \in \Gamma$: transportaion plan
    • $x_1$ 에서 $x_2$로 얼마나 옮겨야 $p_{u_1}$에서 $p_{u_2}$가 되는지..
    • 그 가능한 셋 중에서 한 계획이라 보면 된다.
    • 다음 섹션의 첫번째 table을 참조해서 보자. $x_1 = 0$인 부분에서 0으로 1/6, 1로 2/6을 이동시키고, $x_1 = 1$인 부분에서 0으로 1/6, 1로 2/6을 이동시키면 최종적으로 $p_{\mu_2}$가 된다.

이제 w-distance를 쉽게 정의할 수 있다.

  • $x_1$에서 $x_2$로 옮기는 데, 거리를 $\vert x_1 - x_2\vert$로 생각한거지..
    • mass * distance를 cost로 보아서..
    • 즉 $p_{\mu_1}$에서 $p_{\mu_2}$로 distance를 만드는데 필요한 가장 적은 cost를 구한 것!

여기에 jensen’s inequality를 쓰면 lower bound를 구할 수 있다.

거창하게 말고… $\sum \vert a \vert \ge \vert \sum a \vert $요렇게만 봐도 쉽지.

  • $m_n$: $\mu_n$의 mean

이제 이후에는 이 W-distance의 lower bound를 최적화한다

marginal distribution은 같지만 다른 joint distribution의 예

  • $\mu_1,\mu_2$가 평균이 1/2, 2/3인 bernoulli distribution을 따른다고 가정해보자
  • $\Gamma(\mu_1, \mu_2)$에는 이런 녀석들이 가능
  0 1 $p_{\mu_1}(x_1)$
0 $\frac{1}{6}$ $\frac{2}{6}$ $\frac{1}{2}$
1 $\frac{1}{6}$ $\frac{2}{6}$ $\frac{1}{2}$
$p_{\mu_2}(x_2)$ $\frac{1}{3}$ $\frac{2}{3}$  
  0 1 $p_{\mu_1}(x_1)$
0 $\frac{2}{9}$ $\frac{5}{18}$ $\frac{1}{2}$
1 $\frac{1}{9}$ $\frac{7}{18}$ $\frac{1}{2}$
$p_{\mu_2}(x_2)$ $\frac{1}{3}$ $\frac{2}{3}$  

GAN objective

드디어 GAN을 어떻게 만들까가 나온다..

  • $z \in [-1, 1]^{N_z}$: uniform random samples
  • $G:\textbf{R}^{N_z} \rightarrow \textbf{R}^{N_x}$ generator
  • Discriminator는 (1)번 식을 maximize해야한다.
    • $\vert m_1 - m_2\vert$를 maximize
    • $W_1(\mu_1, \mu_2) \ge m_2-m_1$
    • $m_1 \rightarrow 0$
    • $m_2 \rightarrow \infty$

위 내용을 파라미터를 넣은 수식으로 다시쓰면

  • $\theta_D$: Discriminator의 파라미터
  • $\theta_G$: Generator의 파라미터

일 때

  • $\cal{L}_D = \cal{L}(x;\theta_D) - \cal{L}(G(z_D;\theta_G);\theta_D)$
    • Discriminator의 loss는 작게, Generator의 loss는 크게..(GAN이 맨날 그렇지..)
  • $\cal{L}_G = -\cal{L}_D$

이렇게 만들어서 WGAN에서의 한계인 K-Lipschitz 컨디션이 필요없다고 하는데 이건 나중에 시간나면 알아보자.

그리고, 요렇게 만들었는데 여느때와 같이 D가 G를 압도해버리는 문제가 생겼다. 그래서 Equilibrium을 도입한다.

Proposed Method(Final)

위의 식이 평형상태라고 본다. 당연히… fake data나 real data나 AE의 loss가 비슷하면 평형이다. 근데 좀 더 condition을 relax해보자.

BEGAN에서 Discriminator는 두가지 목적을 가진다.

  1. 진짜 이미지를 잘 AE로 loss 적게 만들기
  2. G에서 나온 것은 loss를 크게 구분해주기

$\gamma$를 작게 세팅하면 진짜 이미지를 잘 decoding하는 것이 목적이며, 따라서 이를 diversity ratio라고 명명했다.

이제 Equilibrium을 넣은 BEGAN의 objective는

가 된다.

  • 맨 처음식
    • $k_t$는 0부터 시작한다.
    • generator의 loss를 얼마나 discriminator에 반영할지 정한다.
  • 두번째 식
    • Generator가 처음에 뱉는 것이 더 reconstruction이 잘됨 -> loss 적음
  • 세번째 식
    • $\lambda_k$ : 0.001부터 시작
    • proportional control theory에서 왔단다.
    • 두려워하지말고 차근차근 뜯어보다…
      • 먼저 처음식에서 k가 커지면 discriminator는 generator가 loss를 크게하도록 최적화하는데 가중치를 둔다.
      • 이제 세번째 식을 보면 실제 이미지의 loss의 감마배보다 fake 이미지의 loss가 크다면
        • 즉 Generator가 잘 못할 것 같으면 -> k값을 줄여서 discriminator가 자기 loss 줄이는데 더 초점을 두도록..
        • fake image의 loss가 작으면, (G가 잘하면) -> k값을 늘려서 g를 견제하도록 해준다.

training을 D와 G에 대해 병렬로 수행할 수 있었으며, pretrained된 D에 대해서도 잘 학습이 됐다!(EQ가 잘됨)

Convergence measure

GAN이 학습이 잘됐는지 끝난건지 measure가 없어서 만들어봄!

  • 앞에꺼
    • real-image를 얼마나 잘 decoding 하나
  • 뒤에꺼
    • proportional control error라는데…

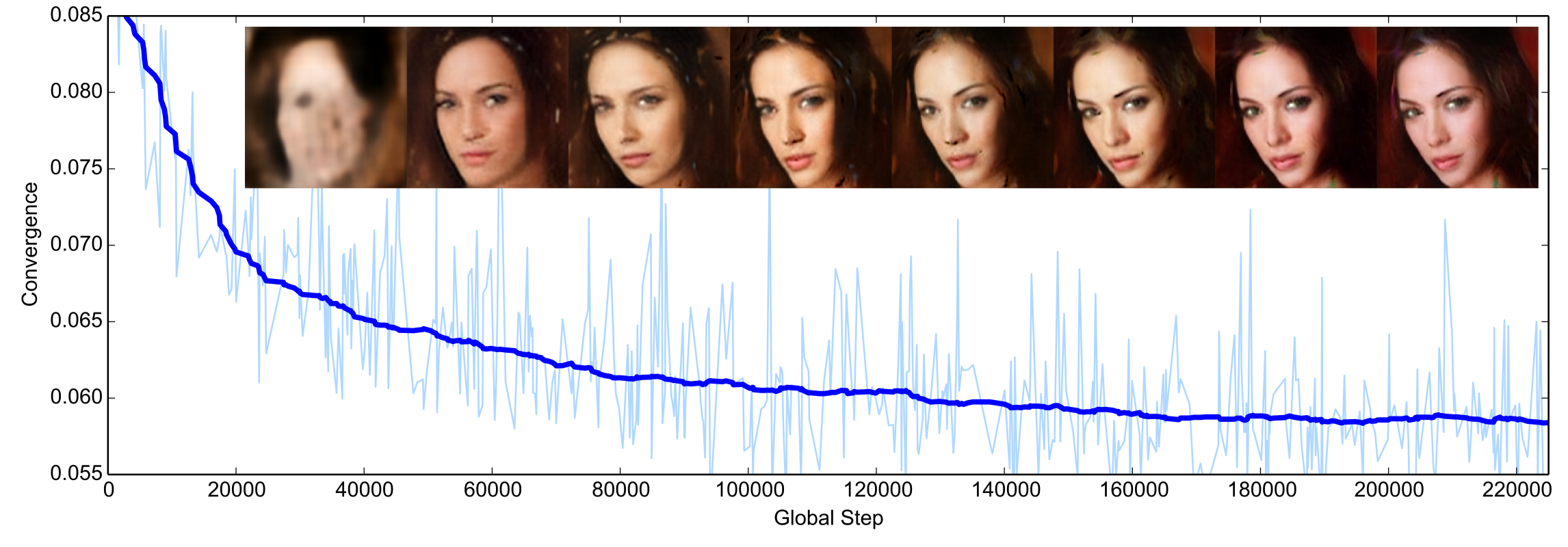
요걸 loss처럼 사용해보면 이렇게 잘 된다고 함 gs.png

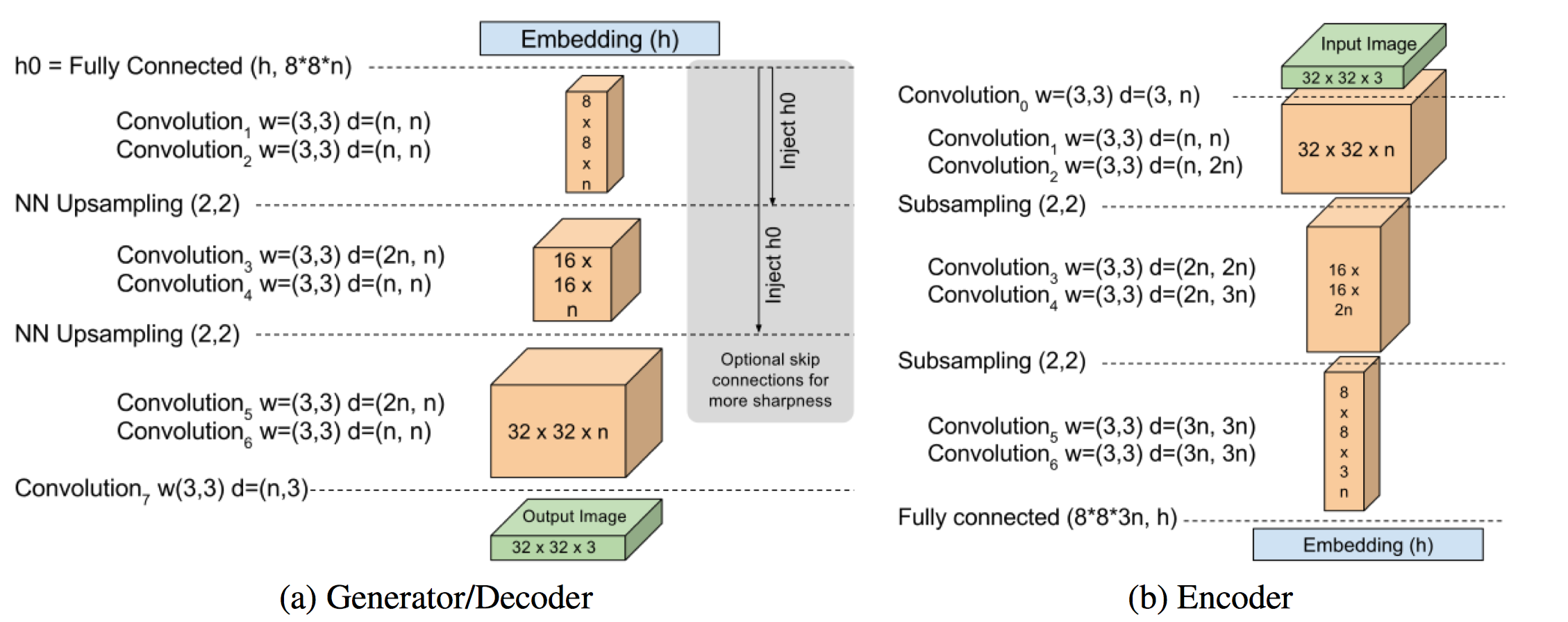
마지막으로 모델 사진

Model.png

나의 생각

  • EBGAN에서 AE를 써서 generator의 gradient를 좀 더 세부적으로 조정이 가능했을 것이다.
  • loss의 distriution 매칭을 강조했는데 이건 EBGAN을 봐야 알겠다..
  • WGAN의 w-distance를 좀 더 파봐야함.
  • 다음엔 unrolled-gan을 볼까 생각이 든다. (이유는 아래 코드 구현에…)

code

  • 내 깃헙에 BEGAN 코드를 만들어 올렸다.
  • mode collapse 문제를 제대로 해결 못했는데 celebA가 다 얼굴이라 피해간 것으로 보이지 않을까 싶다.
  • 그래서 fashion-mnist를 가지고 실험했는데 신발만 학습하거나, 옷만 학습하더라…
  • update: celebA의 데이터는 얼굴 사이사이의 data가 존재(data distribution이 훨씬 더 continuous)하기 때문에 더 잘되는 것으로 결론냄
    • 그렇다면 mnist같이 여러개의 class를 가지고 실험하는 경우는 class별로 separable하니까 하나만 학습될 가능성이 높아짐

Related Posts