참고 0: 요걸 기본으로 해서 이 포스트를 작성!

참고 1: Eric jang의 블로그

Motivation

deep learning에서, 보통 우리는 $x \sim p_\theta(x)$에서 draw한 sample들을 통해 gradient를 backpropagation을 하게 된다.

• 물론 여기서 $p_\theta(x)$는 learned parametric distribution

예를 들어 variational autoencoder(VAE)를 학습한다면, input x에 대해서, latent representation z는 $q_\phi(z \vert x)$에서 오고, 보통 이는

• $q_\phi(z \vert x) = \cal{N}(\mu_\phi(x), \Sigma_\phi(x))(z)$

가 되며, 이 때 $\phi$또한 neural network의 parameter가 된다.

이제 학습을 진행하면 loss의 parameter $\phi$에 대한 backpropagation이 필요하다.

간단하게 얘기를 했는데 VAE 정리를 예전에 해놔서.. 여기에 있음!

Goal

다시 정리하자면 우리는 cost의 기대값을 minimize하는 것이 골인데, 그 cost의 기대값은 다음처럼 표현된다.

gradient descent를 사용해서 이를 달성할건데, 그러려면

• $\nabla_\theta L(\theta,\phi)$
• $\nabla_\phi L(\theta,\phi)$

두가지를 구해야한다.

$\nabla_{\theta}\mathbf{E}_{x\sim p_\phi(x)}[f_{\theta}(x)]$ 계산

이건 항상 하는 일로 굉장히 쉬운데

$\nabla_{\theta} L(\theta, \phi) = \nabla_{\theta}\mathbf{E}_{x\sim p_\phi(x)}[f_{\theta}(x)] = \mathbf{E}_{x\sim p_\phi(x)}[\nabla_{\theta} f_{\theta}(x)]$ 이며 따라서 샘플링으로 쉽게 끝낼 수 있다.

$\nabla_{\theta} L(\theta, \phi) \approx \frac{1}{|S|} \sum_{s=1}^S \nabla_{\theta} f_{\theta}(x_s)$

요렇게….

$\nabla_{\phi}\mathbf{E}_{x\sim p_\phi(x)}[f_{\theta}(x)]$ 계산

요거는 이제 어려워지는데… 수식을 전개해보면

이 되어서 sampling으로 할 수가 없게된다.

요걸 기억하라고한다.

• $p_\phi(x)$가 $\phi$에 대해 미분 가능해야함
• $f_\theta(x)$는 굳이 x에 대해 미분가능할 필요 없음

이제 이 어려운 일을 어떤식으로 파헤쳐나가는지 알아보는 것이 이 포스팅의 목적!

여기까지 한줄 요약: sampling하는 distribution에 대해서 backpropagation(BP)을 하지 않으면 쉽고, sampling하는 distribution에 대해서 BP를 하면 골치아파짐. 그래서 sampling하는 dist.에 대해 어떻게 대처하는지 여러 방법을 알아보려 함.

Score function estimator(SF)

Policy gradient에서 보던 방법이다. integral을 어떻게든 expectation으로 만들어서 sampling가능하게 만들어주는 것이 목적!

고등학교에서 나오던 이 미분식 하나로 모든게 끝난다. $\nabla_{\phi} \log p_\phi(x) = \frac {\nabla_{\phi}p_\phi(x)}{p_\phi(x)}$ 요걸 다시 써보면 $\nabla_{\phi}p_\phi(x) = p_\phi(x) \cdot \nabla_{\phi} \log p_\phi(x)$

위의 식을 이용해서 전개하면

요렇게하면 $p_\phi(x)$에 대해서 expectation꼴이 되므로 아까와 같이 sampling하면 된다.

Reparameterization trick

VAE에서 보던 trick인데, 굉장히 단순하며 잘 작동한다. stochastic node를 stochastic한 부분과 deterministic한 부분으로 분해시켜서 deterministic한 부분으로 backpropagation을 흐르게하자는게 핵심! 즉, $x = g(\phi, \epsilon)$로 deterministic, stochastic의 함수로 본다.

예를 들어보면 $x \sim \cal{N}(\mu_\phi,\sigma^2_\phi)$인 녀석은

• $\epsilon \sim \cal{N}(0, 1)$을 이용하면
• $x = \mu_\phi + \sigma^2_\phi*\epsilon$으로 나타낼 수 있다.

위처럼 stochastic과 deterministic으로 나누면 gradient를 다음처럼 구할 수 있다.

근데 요구조건이 존재한다.

• $f_\theta(x)$가 $x$에 대해 미분가능해야한다.
  • 이 조건은 쉽다. 맨날 하는 일이니…
• $g(\phi, \epsilon)$이 존재해야하며, $\phi$에 대해 미분가능해야한다.
  • 그렇다면 continuous해야하는데, 이는 categorical variable에 대해서는 불가능한가?
  • 그렇진 않다. 이를 가능하게하려면 Gumbel-max trick과 Gumbel-softmax trick을 사용하면 된다.

사실 이 부분을 가장 알고싶어서 시작한 일인데 이제야 Gumbel까지 왔다..

Gumbel-max trick(stochastic을 따로 뺌)

categorical한 variable을 reparametrization함. 요걸 쓰면 categorical에서 sample한 것과 비슷한 효과를 낸다고한다.

$x \sim \cal{Cat}(\pi_\phi)$를 discrete categorical variable이라 해보자.

$\epsilon_k \sim \mathcal{Gumbel}(0,1)$를 가지고 Reparametrization하면

로 쓸 수 있다. 요것이 Gumbel-max trick

• 하지만 아직도 $\phi$에 대해 discrete하며 미분이 불가능하다.

Gumbel-softmax(continuous)

Gumbel-max의 argmax를 softmax로 바꾼 녀석. 이제 미분이 가능해진다.

특성들

• 여기서 $\tau$는 temporature parameter인데
  • 0에 가까워지면 one-hot
  • 무한대로가면 uniform distribution을 갖는다.
• $p(x_k = \underset{i}{max}\ x_i) = \pi_k$

참고 1: Eric jang의 블로그를 보면 MNIST VAE를 Gumbel softmax로 구현한 코드도 존재한다. 이를 보면 좀 더 쉬울 것이다.

참고 구현

잘 안와닿으니까 코드로 보자

import math
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt


def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum()

def sample_gumbel(eps=1e-20):
    u = np.random.uniform(0,1)
    return -math.log(-math.log(u+eps)+eps)


def gumbel_softmax(logits, tau=0.01):
    g = [sample_gumbel() for _ in range(logits.shape[0])]
    y = logits + g
    return softmax(y/tau)

x = np.array([0 ,1, 2, 3])
p = np.array([0.0, 0.2, 0.9, 0.1])

plt.plot(x,softmax(p))

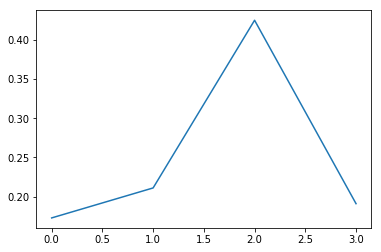
sum_ = np.zeros_like(p)
for i in range(10000):
    sum_ += gumbel_softmax(p)

plt.plot(x,sum_/np.sum(sum_))

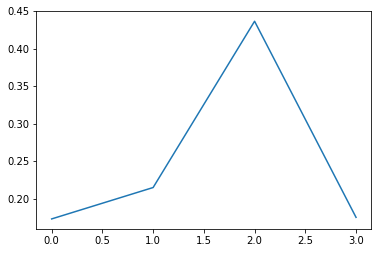
굉장히 비슷함을 알 수 있다!

plt.plot(gumbel_softmax(p))

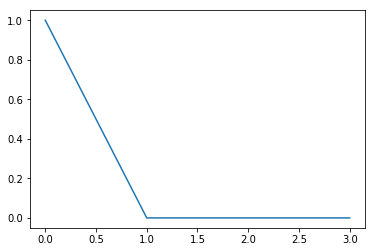
각각의 샘플은 이렇다.