원본

서론

이 페이퍼는 generative model의 배경설명부터 시작한다.

• generative model을 학습시킬 때, data가 어떤 Unknown distribution $P_r$에서 부터 온다고 가정한다.(r은 real을 뜻함)
• 그리고 우리는 그 $P_r$을 근사시키는 $P_\theta$를 학습시키고 싶어한다.(여기서 $\theta$는 parameter)
• 이제, 이를 만족시키는 두가지 방법을 찾을 수 있는데,
  • $P_\theta$를 직접 학습시킨다: MLE를 통해 $P_\theta$를 학습
  • 어떤 다루기 쉬운 distribution $Z$에서 $P_\theta$로 가는 transform function을 학습한다.
    • 보통 이때 $Z$는 Gaussian dist를 쓴다.
    • $P_\theta = g_\theta(Z)$
• 이제 처음 방법의 문제를 설명해보자.
  • $P_\theta$가 주어졌을 때, MLE objective는
    • $$\underset{\theta \in R^d}{max}\frac{1}{m}\sum_{i=1}^{m}logP_\theta(x^{(i)})$$
    • 그리고 이는 m을 무한대로 보내면 KLD와 같다

      • $$\begin{aligned} \lim_{m \to \infty} \max_{\theta \in \mathbb{R}^d} \frac{1}{m}\sum_{i=1}^m \log P_\theta(x^{(i)}) &= \max_{\theta \in \mathbb{R}^d} \int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} -\int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} \int_x P_r(x) \log P_r(x) \, dx -\int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} KL(P_r \| P_\theta) \end{aligned}$$

  • $P(x) \ge 0$인 어떤 x에서 $Q(x) = 0$이면 KLD가 무한대로 감
  • This is bad for the MLE if $P_\theta$ has low dimensional support, because it’ll be very unlikely that all of $P_r$ lies within that support.(뭔말인지…wiki를 보면 0이아닌 domain의 subset을 말하는 것 같다.)
  • 아니면 학습 시, random noise를 주는 방법도 존재!
    • distribution이 어디서는 정의되어있다는 것을 보장해주나, 학습시에 random noise를 뿌리는건 별로다.(정말?)
  • 그래서 두번째 방법으로 구현을 하게된다.
• 두번째 방법
  • inference 방법
    • $z \sim Z$ sample
    • $g_\theta(Z)$로 evaluation
  • $g_\theta$를 학습시키기 위해 distribution들의 거리를 재는 measure가 필요하다.

여러 Distance들

• total variation(TV)
  • $\delta(P_r, P_g) = \sup_{A} \vert P_r(A) - P_g(A) \vert$
  • 두 dist에서 벌어질 수 있는 값중 가장 큰 값
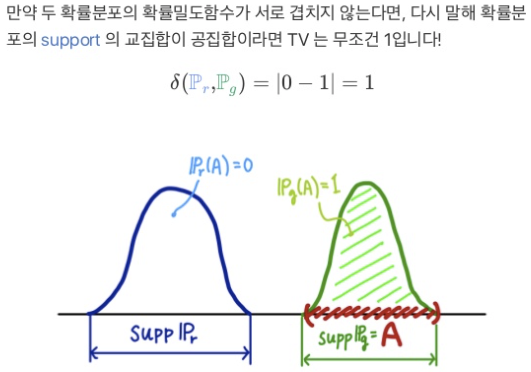  • 참고…
• KL-divergence(KLD)
  • $KL(P_r|P_g) = \int_x \log\left(\frac{P_r(x)}{P_g(x)}\right) P_r(x) \,dx$
• Jenson-shannon-divergence(JSD)
  • $JS(P_r,P_g) = \frac{1}{2}KL(P_r|P_m)+\frac{1}{2}KL(P_g|P_m)$
• W-distance(EM-dist)
  • $W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[||x - y||\big]$
  • 여기를 보자 BEGAN

Next: 근데, 이 녀석들을 보니까 W-distance 빼고는 전부 너무 hard한 녀석들! (distribution이 겹치지 않으면 불연속이 된다.) 그래서 W-distance를 쓴다.

example

다음과 같은 distribution을 보자. $R^2$에 대해서 정의되어있으며, 실제 distribution은 $(0,y)$인데, $y \sim U[0,1]$이라 하며, $P_\theta=(\theta, y)$라 하자. 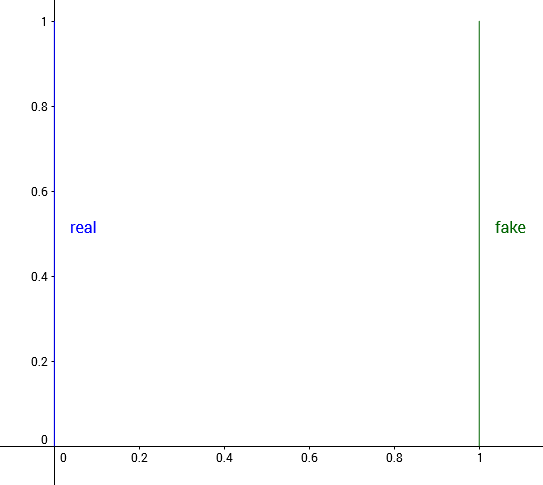이제 우리가 하고픈 일은 $\theta \rightarrow 0$으로 이동시켜서 distance를 줄어들게하는 것이다.

• Total variation: $\theta \neq 0$에 대해, $A = { (0, y) : y \in [0,1] }$ 를 이렇게 정의하면

  • $$\delta(P_0, P_\theta) =\begin{cases} 1 &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~. \end{cases}$$
• KLD
  • $$KL(P_0 \| P_\theta) = KL(P_\theta \| P_0) =\begin{cases} +\infty &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~, \end{cases}$$
• JSD
  • $$JS(P_0, P_\theta) = \begin{cases} \log 2 &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~, \end{cases}$$
• EMD
  • $P_\theta$는 $P_r$의 translation이기 때문에, $(0, y)$에서 $(\theta, y)$로 옮기는 가장 좋은 plan은 $\vert \theta \vert$이다.
  • 이건 연속적이네???

그래서 W-gan에서는 EMD를 써서 학습을 잘 시키도록 했다는 말..

Wasserstein GAN

• 근데 사실 W-distance가 intractable하다.
  • $W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[||x - y||\big]$
• 그래서 이를 근사시켜서 푼다
  • $$W(P_r, P_\theta) = \sup_{\|f\|_L \leq 1} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_\theta}[f(x)]$$
  • f가 1-lipshcitz 함수여야함 (기울기가 1을 넘지 않는 함수)
  • 근데 이를 K-lipshcitz 함수로 바꿔도 문제가 안생긴다고 함…
  • 대충 그러면
    • $\theta$를 고정시키고 $f_w$를 수렴시킨다
    • 구한 $f_w$와 새로 샘플링한 $z$로 $-E_{z \sim Z}[\nabla_\theta f_w(g_\theta(z))]$를 구하고 gradient를 구한다
    • $\theta$ update

알고리즘