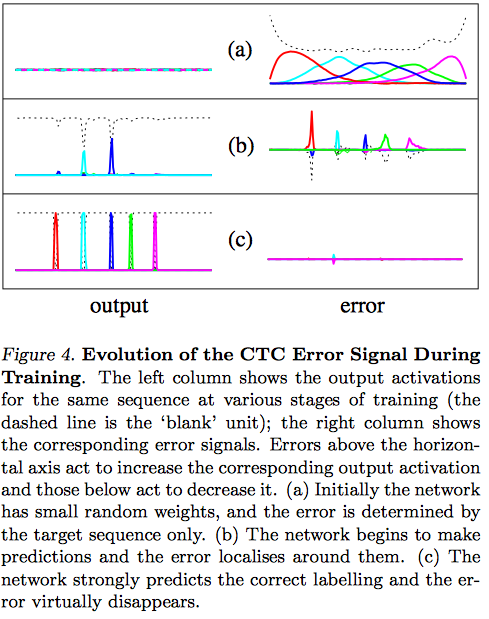
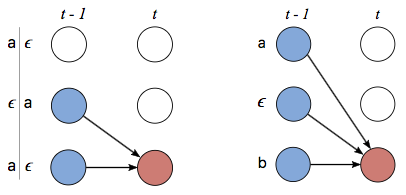
Connectionist Temporal Classification
30 Jan 2018 | ml rnn배경 설명
- RNN은 sequence learning을 잘 할 수 있음
- 근데 segmentation이 안되어있으면, 학습이 힘들다.
- 그래서 segmentation을 하려고 하니 데이터를 많이 만들기 힘들다.
- 아래 그림처럼 unsegmented data를 바로 학습할 수는 없을까?
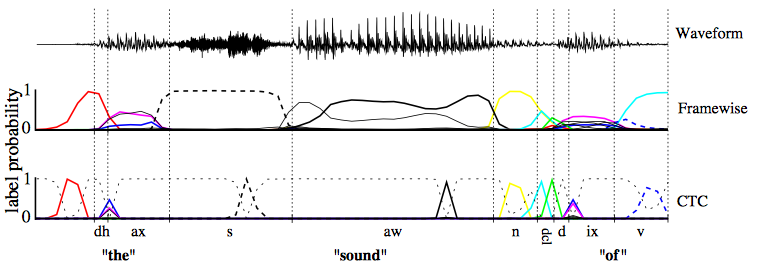
접근방법
- input도 variable, output도 variable인데, 가능한 align을 모두 뽑아서 marginalize하면 됨!
2. Temporal Classification
Temporal domain에 있는 것들을 classify하기 위한 정의 (Kadous, 2002)
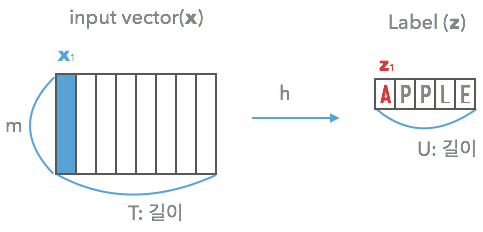
- input space $\cal{X} = (\mathbb{R}^m)^*$
- $m$차원 vector의 sequence.
- $\cal{Z} = L^*$
- label의 sequence겠지..
- $S$
- 고정된 distribution $D_{\cal{X} \times \cal{Z}}$에서 뽑힌 학습셋
라고 하면 $S$는 $(\textbf{x}, \textbf{z})$들로 이루어져있지.
- $\textbf{z} = (z_1, … , z_U)$
- $\textbf{x} = (x_1, … , x_T)$
$U \le T$ 여야함. 나중에 CTC_LOSS 정의를 보면 알겠지만..
목표
$S$를 사용하여 $h: \cal{X} \rightarrow \cal{Z}$를 학습시킴
2.1. Label Error Rate(LER)
- $S’ \subset D_{\cal{X} \times \cal{Z}}$를 S와는 다른 test set이라 하고,
- $Z$는 $S’$의 전체 갯수라 하면
여기서 $ED$는 Edit distance이다.
3. Connectionist Temporal Classification
- alignment를 이용해보자!
RNN과 blank를 이용
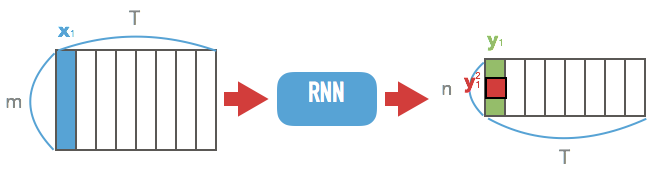
- $\cal{N}_w$: m차원 vector를 n차원으로 줄이는 RNN
- $\textbf{x}$를 넣으면
- $n\times T$의 matrix가 나옴.
- 이제 $\textbf{y} = \cal{N}_w(\textbf{x})$라 하면
- $y_k^t$: t번째 step의 k번째 label의 probability
-
$L’$는 $L$에서 blank가 추가된 것!
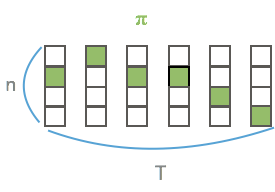
many-to-one map $\cal{B}$
- $\cal{B}$: $L’^T \rightarrow L^{\le T}$
- $L^{\le T}$: 가능한 labeling의 집합.
- 방식: blank와 반복되는 label을 제거
- $\cal{B}(a−ab−) = \cal{B}(−aa−−abb) = aab$
- 요렇게 되면 당연히 many-to-one의 관계!
이제 위의 $\cal{B}$를 통해 $\textbf{l} \in L^{\le T}$의 probability를 구할 수 있다!!!!
-
- label $\textbf{l}$에 해당하는 모든 $\pi$에 대해서 summation을 하면 된다.
3.2. Constructing the Classifier
여기까지 했으면 $h$는 단순히 다음처럼 끝난다.
$\textbf{l}$을 가능하게 하는 모든 path들의 확률을 더해서 이 중 argmax를 찾음.
- 아쉽게도, 이 수식에는 many-to-one인 $\cal{B}$의 역함수를 쓰게되며, 계산이 어려워진다.
- 따라서 approximation을 쓰게되는데, 다음 두가지가 존재한다.
- $h(\textbf{x}) \sim \cal{B}(\pi^*)$
- where
- 수식으로 보니까 헷갈리지만 단순히 RNN에서 max probability를 뽑고, 그것을 $\cal{B}$에 태운 것!
- prefix search decoding
- 4.1에서 설명할 forward-backward algorithm을 수정한 것
- 계산시간이 느림…
- 좋은 방법 없나?
- dynamic programming으로 해결한다.
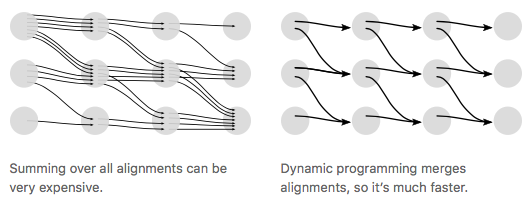
- 사진 출처
- $h(\textbf{x}) \sim \cal{B}(\pi^*)$
4. Training the Network
4.1. The CTC Forward-Backward Algorithm
$p(\textbf{l}\ \vert\ \textbf{x})$를 구하는 효율적인 알고리즘!
forward variable $\alpha_t(s)$
엄청 헷갈려 보이나 잘 뜯어보면
- Summation 아래:
- $N^T$: $\pi$의 1~t까지가 label의 1~s를 만족하는 path의 set
- 그 안의 $\pi$에 대해서 summation
- Pi는:
- 그 path의 확률을 전부 곱해준 것
결국 $\alpha_t(s)$란 1:t까지 가면서 label $\textbf{l}_{1:s}$를 만들 확률을 의미한다.
이제 label의 각 사이사이와 앞, 뒤에 blank를 붙여서 $\textbf{l}’$를 만들고 이 녀석에 대해서 forward 계산을 할 것이다.
나중에 보면, 이렇게 해야 여러 path가 나온다.
그러면
- $\alpha_1(1) = y_b^1$
- $\alpha_1(2) = y_{\textbf{l}_1}^1$
- $\alpha_1(s) = 0\ \ \ \ \ \forall s > 2$
이며 자연스럽게 아래 triangle은 0가 된다.
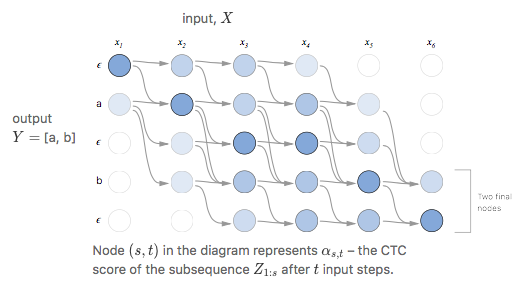 사진 출처
사진 출처
그리고 recursion을 할 수식은 다음과 같다.
- 여태까지 설명한 것은 forward를 구하는 방법인데, 이는 사실 network output의 1:t가 label의 1:s일 확률을 구했다고볼 수 있다.
- $t:T$가 label의 $s:\vert l\vert$일 확률을 구하는 것이 backward인데, 이는 forward와 수식전개가 거의 똑같으므로 딱히 설명하지 않겠다.
- $\beta_t(s)$로 표기한다는 것만 알아두자.
또 underflow를 방지하기위해 각자 normalize해서 쓴다고한다. 별 중요한 얘기는 아님
4.1. Maximum Likelihood Training
forward-backward variable로 $p(\textbf{l} \vert \textbf{x})$ 표현하기
- 이제 forward-backward를 곱하고 $y_{\textbf{l’}_s}^t$로 나누면 (s자리는 겹치니까.. 당연히 나눠줘야지)
- 번역해보면 t번째 output이 label의 s번째일 때, label이 나올 확률
- 그러면
- 그래서 미분하면…
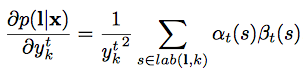
MLE 계산
- 이제 실제로 gradient를 구해보자
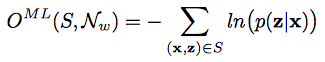
- 요걸 $(x,z) \in S$에 대해서 미분하면..
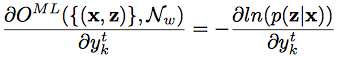
- 위의 식을 요걸로 치환하고, $\textbf{l} = \textbf{z}$니까..
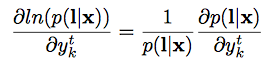
- 요렇게 된다고 한다.(귀찮아서 안따라가봄… $u_k^t$는 $y_k^t$의 unnormalized probability.
오타가 아니다) 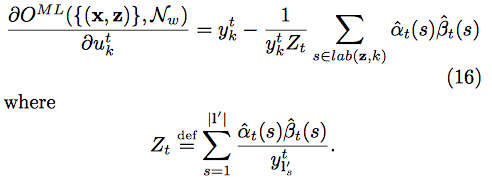
- 여기서 (16)은 error signal로, 학습중에 유용하게 쓰인다고 함