논문 링크

ASTER: An Attentional Scene Text Recognizer with Flexible Rectification

• irregular text에 대해서 잘 인식해보겠다.
• 두가지 네트워크로 구성
  • 
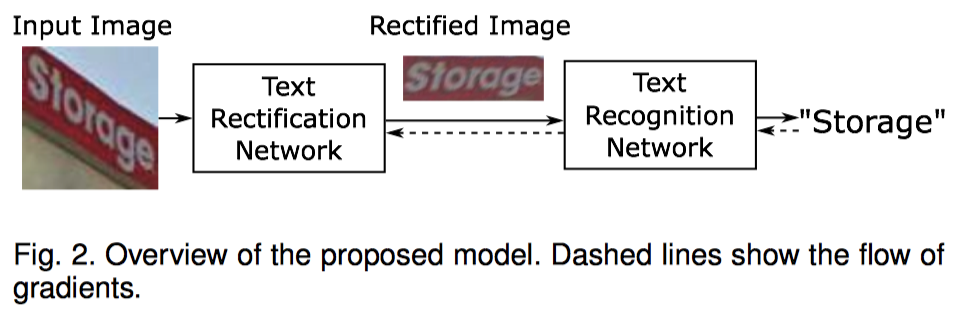
  • Rectification network
    • Thin-Plate Spline의 parameter를 추정하고 이를 통해 transformation
    • Spatial Transformer Networks framework로 annotation 없이 바로 학습 가능 (모두 미분 가능)
    • input: 64 x 256 으로 resize
    • output: 32 x 100
    • sampler는 여기 참조
  • Recognition network
    • Attentional seq2seq
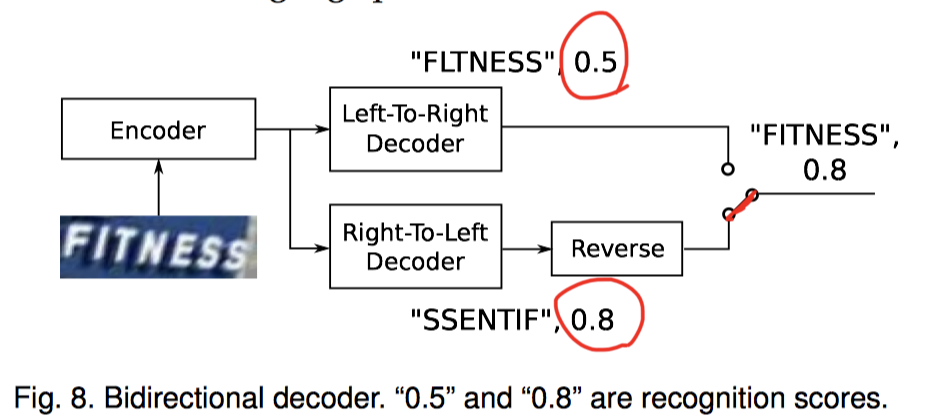
    • Decoder를 BiDirectional로 만듬
• Contributions
  • irregular text 문제를 explicit rectification mechanism을 사용해서 풀었다.
  • bidirectional decoder를 만듬
    • 뒤에서부터 볼 때 더 context가 좋을 수 있음
    • 예> FITNESS 에서 I를 알려면 FI 보다 SSENT가 더 좋다.
      • 
  • ASTER를 사용해서 text detection을 더 잘할 수 있는 방법 제시
• conference version보다 더 좋게 만듬
  1. rectification network를 고쳐서 성능을 올림
     1. control points prediction과 sampling에 다른 화질의 이미지를 사용
     2. localization network의 non-linear activation을 없애서 수렴을 더 빨리하도록
        • 결과적으로 accuracy, rectified image quality, sensitivity가 좋아짐
  2. bidirectional
  3. end2end application을 해봄
• 결과
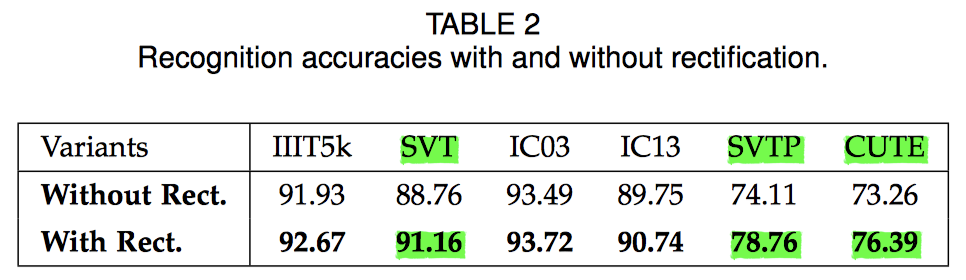
  • rectifier를 넣어보니 SVTP, CUTE 등 irregular text에 대한 dataset에 대해서 3~4% 올라가더라..
    • 

Appendix

Cubic spline interpolation

Thin-plate spline transformation에 앞서 1D interpolation 기법인 Cubic spline interpolation을 알아보자

• Cubic
  • line을 3차식으로 근사시키겠다
  • $f(x) = a + bx + cx^2 + dx^3$
• spline
  • 복수의 제어점을 통과하는 곡선.
  • 인접한 두 점마다 별도의 다항식을 이용하여 곡선을 정의
• Cubic spline interpolation
  • interpolation을 하는데, cubic spline을 이용한다.

how to calculate?

• 각 line을 3차식으로 놓으면 변수가 4개씩 생김
• 인접한 line은 1차, 2차 미분이 연속적임. $C^2$
• 각 line은 주어진 점을 지남
• 위 두가지 constraint + boundary condition으로 연립 방정식을 풀면 된다.
  • natural cubic spline
    • 양 끝 라인의 이차미분값이 0
  • clamped cubic spline
    • 양 끝 라인의 일차 미분값이 주어짐

Cubic spline transformation

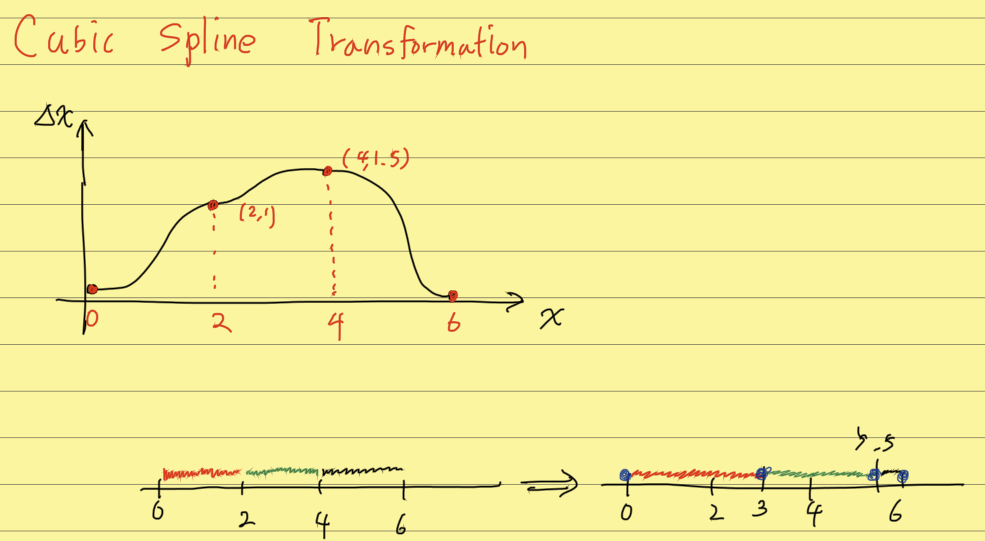
• 위의 빨간 점들이 1차원 라인에 대한 변위량을 나타낸다고 하면
• Cubic spline interpolation을 사용하여 검은 선을 만들 수 있다.
• 검은 선들을 통해서 변화된 1차원 라인을 만들 수 있음.

Thin plates

• 얇은 판이 휘어지는 것으로 interpolation을 함.
• $ f(x,y) = a_1 + a_2x + a_3y + \Sigma_{i=1}^{n}w_i U(\vert P_i-(x, y) \vert ) $
  • $U(r) = r^2log(r)$
• 더 자세한 내용은 여기 참조