Hulk의 개인 공부용 블로그

Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels 간단리뷰

19 Aug 2019 | ml loss

논문 링크

두줄 요약

  • Categorical cross entropy(CCE)는 학습이 빠르지만 noise에 민감하고, mean absolute error(MAE)는 noise에 robust하지만 학습이 느리니, 중간 지점을 찾아보자!
  • 요것만으로는 잘 안됐던지, EM 비슷하게 data pruning을 두어서 noisy한 데이터를 자동으로 버리게 해보자!

어려운 얘기들도 많고, 히스토리가 많아서 모든 내용을 담진 못했다. 생략된 부분은 궁금하면 논문을 찾아보자!

  • noisy label data로 잘 학습을 시켜보려고 이런저런 시도가 많았다. 나중에 궁금하면 좀 더 파보자.
    • confusion matrix를 만들어서 시도
      • $p(\hat{y} = \hat{y_n} \vert x_n, \theta) = \Sigma_{i=1}^c p(\hat{y} = \hat{y_n} \vert y = i) p(y = i \vert x_n, \theta)$
      • 여기서 $p(\hat{y} = \hat{y_n} \vert y = i)$를 confusion matrix의 $(\hat{y_n}, i)$를 사용
      • confusion matrix를 유추하는 여러가지 시도가 있었다함. 내가 원하는건 아니니 넘어가자
    • svm과 같은 맥락에서, unhinge loss 등 loss를 좀 더 lobust하게 바꿔보려는 시도가 있었고 그 중 MAE가 제일 robust하더라..
    • label cleaning network를 두어서 해보려는 시도가 있었는데 clean label dataset이 필요함.
    • true label을 latent variable로 두고 EM 알고리즘 비슷하게 찾아보자…

$L_q$ loss for Classification

  • CCE
    • $L(f(x_i; \theta), y_i) = -\Sigma_{i=1}^c y_i log(f_{y_i}(x_i ; \theta)) = -log(f_{y_i}(x_i ; \theta))$
  • MAE
    • $L(f(x_i; \theta), y_i) = \Sigma_{i=1}^c \vert y_i -f_{y_i}(x_i ; \theta) \vert = 2 - 2 f_{y_i}(x_i;\theta)$

이므로 loss를 미분해보면

  • CCE의 경우
  • MAE의 경우

가 된다. CCE의 경우, MAE에 비해 $\frac{1}{f_{y_i}(x_i ; \theta)}$ term이 더 붙는데 이로 인해서 두가지의 장단점이 확연해진다. $f_{y_i}(x_i ; \theta)$가 작다는 말은, prediction이 잘 안되었다는 말이며,

  • 클린한 label일 경우
    • 어려운 예제라는 말인데, 그 것에 대해서 CCE의 경우 더 가중치를 두게되며, MAE는 공평하게 gradient를 흘리게 된다.
    • 그래서 CCE가 더 빨리 학습을 잘하게 된다. (CCE의 장점)
      • 라기보다 MAE가 더럽게 느리다
  • noisy한 label의 경우
    • CCE는 그래도 더 가중치를 두게되며, 학습을 망치게 된다 (CCE의 단점)
    • 상대적으로 MAE는 더 잘 학습한다.

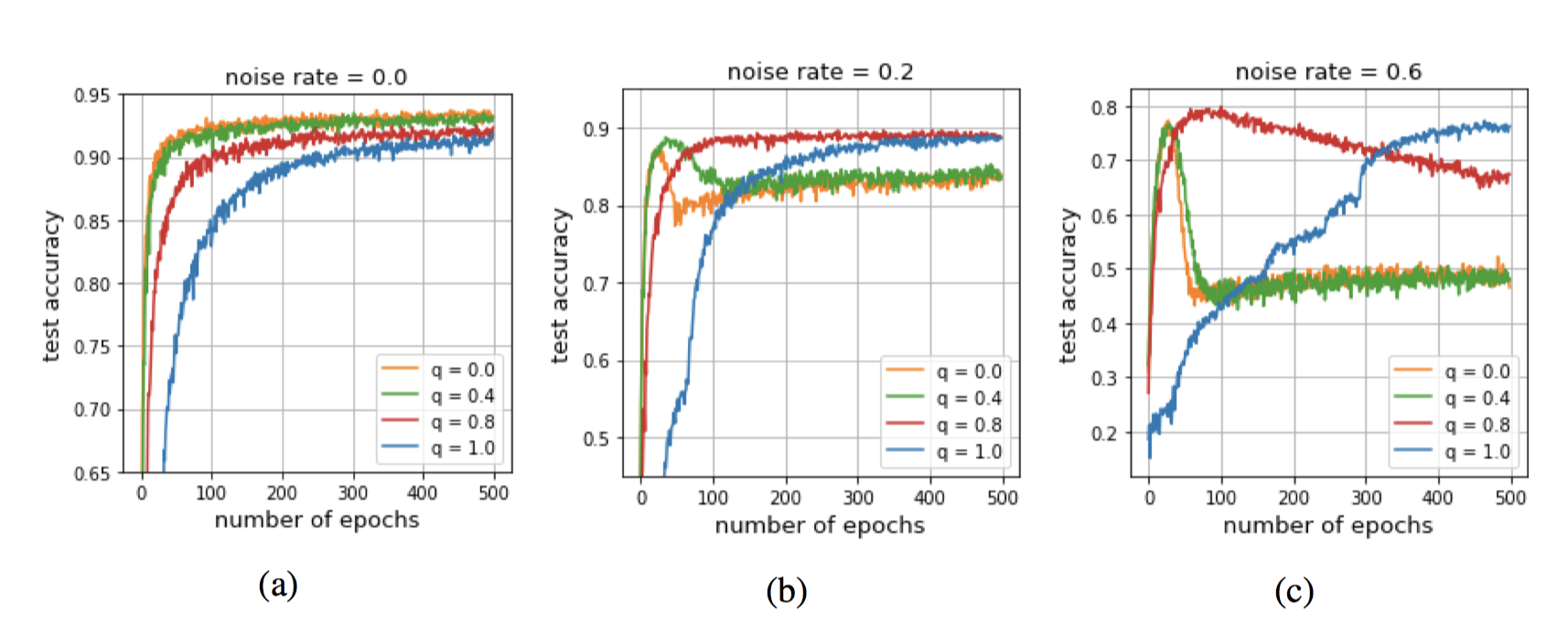
요 사이의 임의의 loss function을 만들어보자가 이 논문의 아이디어!

$L_q$ loss

으로 디자인하면 ${lim}_{q\rightarrow 0}L_q$는 CCE와 같으며, $q=1$에서는 MAE와 같다(정확히는 constant배 차이는 난다)

$q=1$은 당연하니 $q\rightarrow 0$일 때를 보인다. 로피탈 정리를 사용하면 간단히 보일 수 있다. ${lim}{q\rightarrow 0} \frac{1-f^q}{q} = {lim}{q\rightarrow 0} \frac{(-f^q)’}{1} = {lim}_{q\rightarrow 0} (-f^q log{f}) = -log{f}$

이제 이 녀석을 $\theta$에 대해서 미분해보면 일반화된 gradient를 볼 수 있다.

위의 식에서 $(q-1)$ 부분에 따라서 얼마나 noise에 robust할지, 학습을 빠르게할지 정할 수 있게 되는 것!

Truncated $L_q$ loss

그러나 위의 것만으로는 만족할 만한 결과를 못얻었나보다.. true label의 confidence가 k 이하일 경우에는 loss를 $L_q(k)$로 두어서 truncate를 시키도록 하였다.

실험을 통해 k의 값은 0.5로 고정을 하였다고 한다.

만약 k보다 softmx 값이 작으면, $L_{trunc}$가 constant이며, 따라서 gradient는 0가 되어 학습을 하지않는다.

문제는 처음부터 k가 크면, 처음엔 softmax 값이 균등하게 나오고, k보다 모두 작을테니 학습이 진행되지 않을 것이다. 따라서 요런 방식으로 풀어버린다.

w_i

algorithm

Alternative convex search라는데, local하게는 DNN이 convex할꺼라고 가정하고 썼다고 한다. 모든 data sample에 대해서 $w_i=1$로 뒀는데, EM처럼 중간중간에 pruning을 거쳐 noisy data를 걸러내게 되는 것 같다.

결과

result

Related Posts