Hulk의 개인 공부용 블로그

Stand-Alone Self-Attention in Vision Models

10 Sep 2019 | ml building-block attention

논문 링크

  • Attention을 이용해서 Convolutional block들을 대체해보자!

2. Backgrounds

2.1. Convolutions

  • input: $x \in R^{h \times w \times d_{in}}$
  • Weight: $W \in R^{k \times k \times d_{out} \times d_{in}}$
  • local neighborhood: $N_k$
    • $x_{ij}$ 근처의 pixel들
    • $k \times k \times d_{in}$
  • output component: $y_{ij} \in R^{d_{out}}$
    • $y_{ij} = \sum_{(a, b) \in N_k(i, j)} W_{i-a, j-b}x_{ab}$
      • $N_k(i, j) = {a, b \vert \vert a-i \vert \le k/2, \vert b-j\vert \le k/2}$

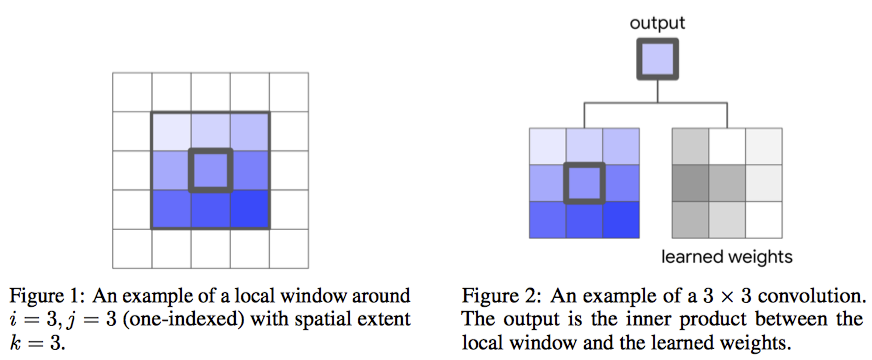
그림으로 보면 간단!

CNN

2.2 Self-Attention

  • stand-alone self-attention layer를 정의
    • spatial convolution들을 대체해보자!
  • Memory-block
    • $x_{ij}$가 주어지면 local region을 뽑아서 memory-block이라 하자.
    • $a,b \in N_k(i, j)$
  • 그러면 요런 식으로 정의가 가능
    • $y_{ij} = \sum_{(a, b) \in N_k(i, j)} softmax_{ab}( { q_{ij} } ^T k_{ab})v_{ab}$
    • $q, k, v$는 attention의 query, key, value를 의미한다.
      • $q_{ij} = W_Qx_{ij}$
      • $k_{ab} = W_Kx_{ab}$
      • $v_{ab} = W_Vx_{ab}$
  • 물론 실제로는 multi-head를 쓴다.

이것도 그림으로 보면 간결하다.

CNN

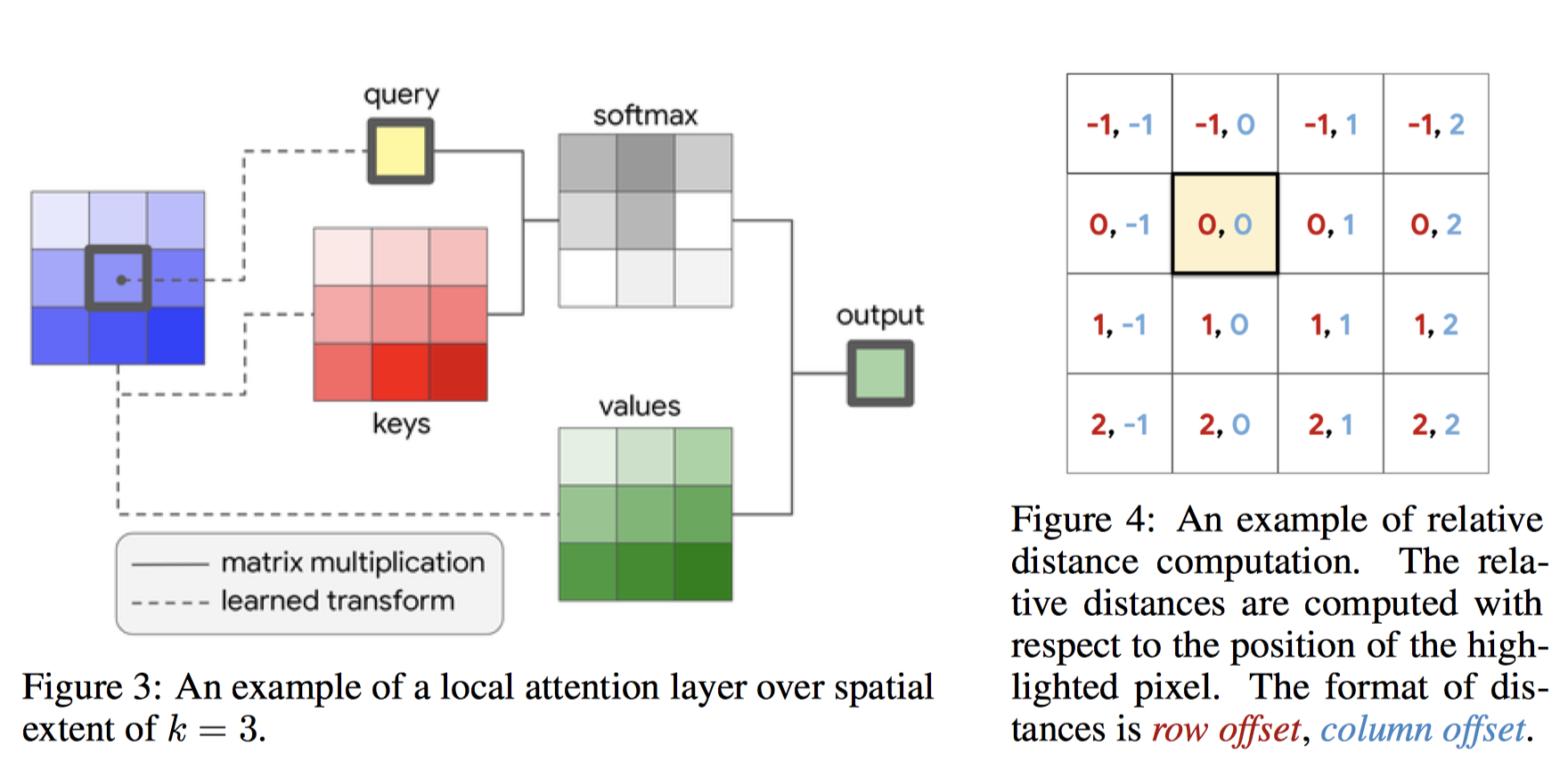
  • 그러나, 인접한 pixel들의 위치정보가 빠지기 때문에 relative positional embedding을 사용하면 더 좋다.
  • row, column에 대해서 $\frac{1}{2}d_{out}$씩 만들고 concat하면 됨
    • 그 녀석을 $r$이라 하면
    • $y_{ij} = \sum_{(a, b) \in N_k(i, j)} softmax_{ab}( { q_{ij} } ^T (k_{ab} + r_{a-i, b-j}))v_{ab}$
    • $r$은 learned parameter로 주는 듯..

이렇게 하면, In/Out channel이 128일 때, k=3인 convolutional layer와 같은 파라미터 갯수로 k=19인 layer를 만들 수 있다고 한다.

3. Fully Attentional Vision Models

위에서 정의한 local attention layer를 primitive로 삼아서, 어떻게 fully attentional architecture를 만들 수 있을까?

3.1 Replacing Spatial Convolutions

  • k > 1인 convolution을 spatial convolution이라 정의하자.
    • 1x1 convolution은 fully connected layer로 볼 수 있으니…
  • 모든 spatial convolution들을 attention layer로 바꿀 수 있다.
  • pooling같은 건 stride 2짜리 2 x 2 average pooling을 뒤에 넣음
  • ResNet family들을 바꿔봄
    • bottleneck block의 3x3 CNN을 바꿈
    • 나머지는 보존

3.2 Replacing the Convolutional Stem

  • CNN의 처음 몇 layer들은 stem이라 불림
    • edge같은 local feature들을 배움
  • input image가 크기 때문에, stem은 보통 core block과 다르게 light-weight operation으로 이루어짐
    • ResNet같은 경우 stride 2인 7 x 7 convolution + stride 2인 3 x 3 maxpooling으로 이루어짐
  • stem의 input은 개별로는 정보가 별로 없고 공간상에 강하게 correlation이 있음
    • 그래서 self-attention이 퍼포먼스가 낮았음.
  • $v_{ab}$를 뽑는데에도 position 정보를 넣었더니 잘 되더라…
    • $v_{ab} = ( \sum_m p(a,b,m) W_V^m ) x_{ab}$
      • $p(a, b, m) = softmax_m((emb_r(a) + emb_c(b))^Tv^m)$
      • $v^m$: per-mixture embedding
    • 잘 이해가 안되는데, 결과를 보면 stem은 그냥 cnn을 쓰는게 낫더라…Skip!

4. Experiments

4.1 ImageNet Classification

  • ResNet-50 모델
  • stem과 spartial conv 모두 바꿔보면서 실험함
  • stem은 CNN 쓰는 것이 제일 낫더라..
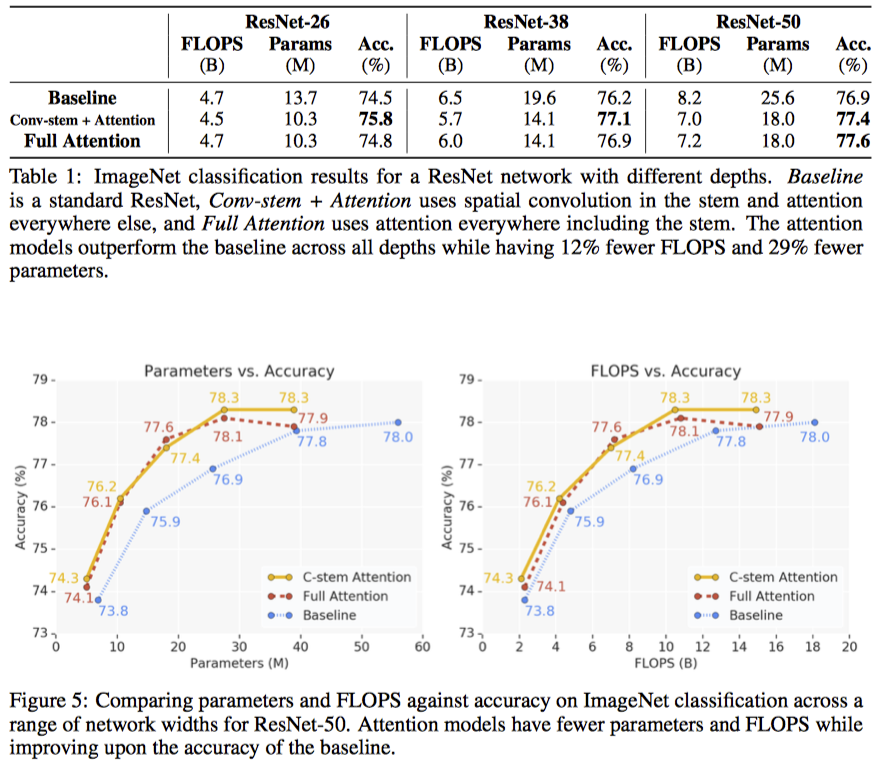
  • FLOPS 12%, parameter 29%정도 내릴 수 있었다.

result1

4.2 COCO Object Detection

  • RetinaNet 모델
  • Backbone과 detection head등을 바꿔가면서 실험

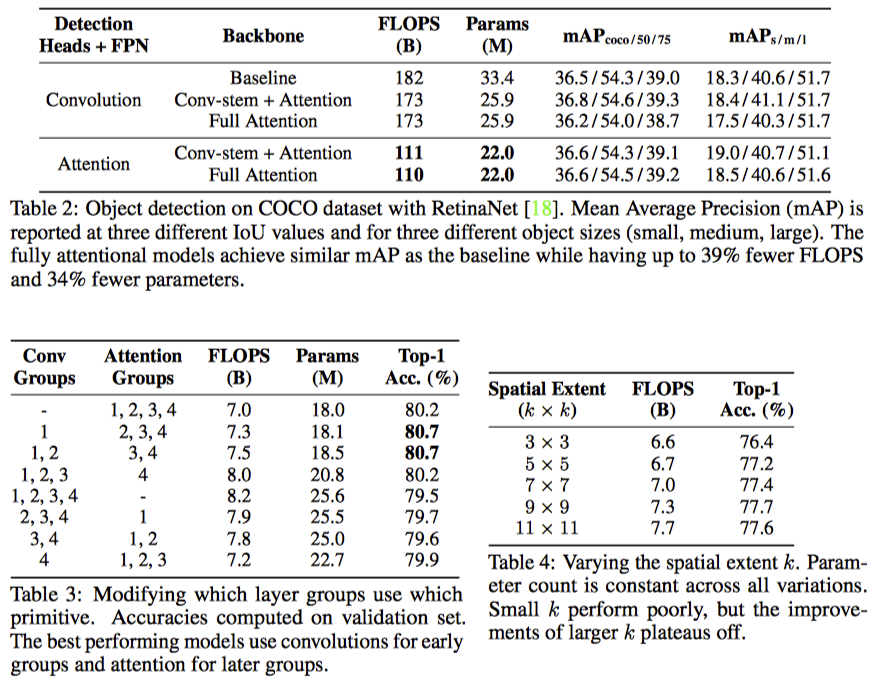
result2

4.3 Where is stand-alone attention most useful?

stem

  • classification에서 CNN stem이 일관되게 더 좋더라
  • object detection에서 detection head와 FPN이 convolution일 때는 CNN이 더 좋고,
    • Attention일 경우에는 비슷하더라.
  • CNN stem을 쓰자

full network

  • Table 3을 보면 역시 앞쪽에 CNN을 쓰고 뒷쪽에 attention을 쓰는 것이 좋더라..
    • 반대의 경우는 오히려 떨어짐

4.4 Which components are important in attention?

  • relative positional embedding이 제일 좋고,
  • $q^Tr$이 있어야 성능이 올라가더라..
  • stem을 positional한 value를 가지고 하는게 좋다

result3

Related Posts