word2vec에는 두가지 방식의 네트워크 모델이 주어진다.

• CBOW
  • 여러 단어를 보고 한단어 맞추기
• Skip-gram
  • 한 단어보고 연관된 여러단어 맞추기

CBOW

one-word context

bigram처럼 한번에 한 단어만 보고 다음 단어를 유추한다.

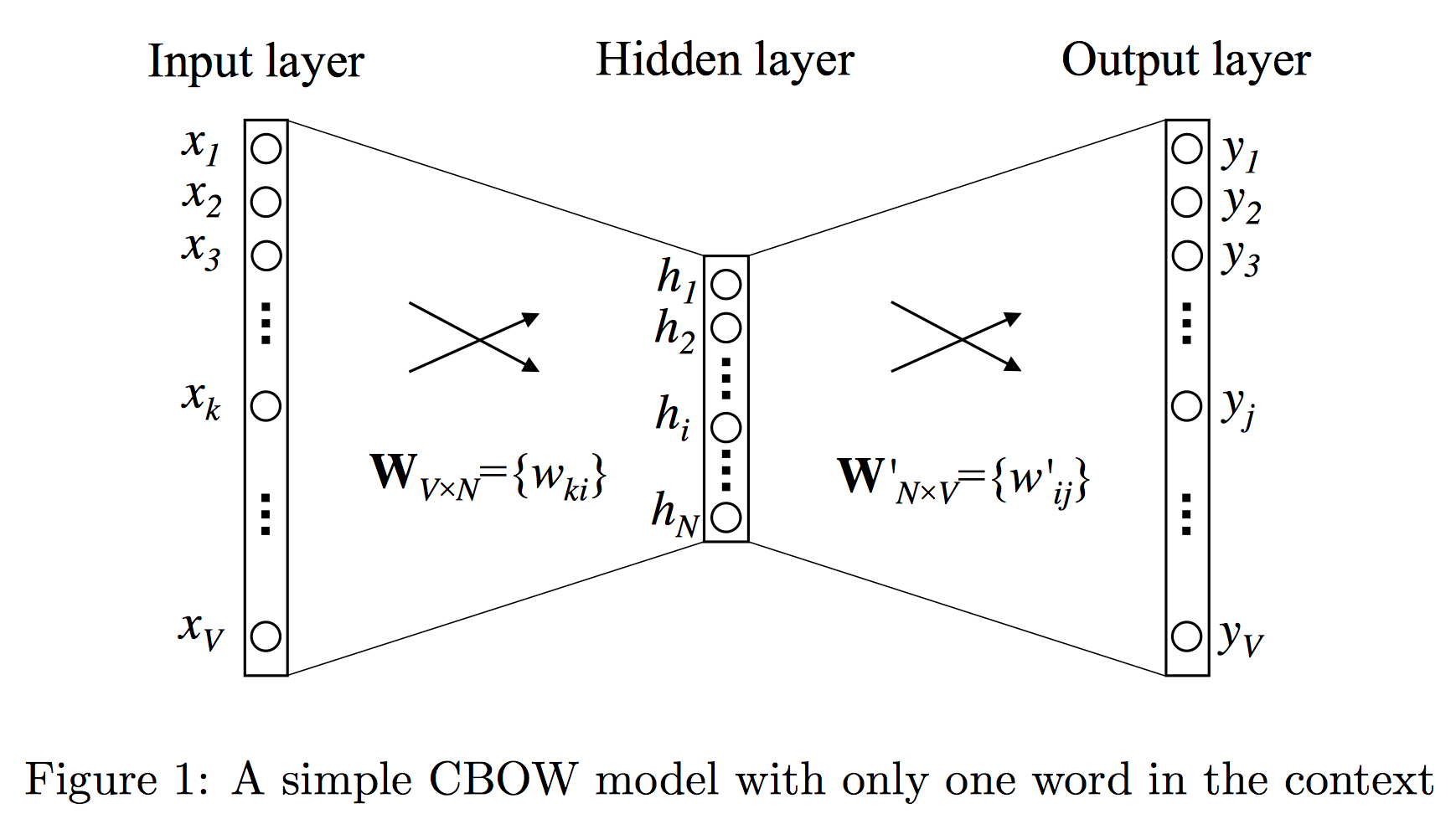
이 그림은 왼손잡이용!

Input -> Hidden layer

• $\mathbb{x}$
  • $V\times 1$인 input vector(one-hot)

이제, Hidden layer로 보내기 위해 matrix $\mathbb{W}$를 거친다.(where size: $N \times V$)

그러면 $\mathbb{h} = \mathbb{W}\mathbb{x}$는

• hidden layer의 output이며
• $k$번째 word에 대한 $\mathbb{h}$는 $\mathbb{W}_{(:,k)}$이다.
• word $w_I$에 대한 vector representation이라 볼 수 있다.
  • $\mathbb{v}_{w_I}$로 쓴다.

Hidden -> Output layer

$\mathbb{W}' = \{w'_{ij}\}$를 size $V \times N$인 hidden->output layer로 보내는 녀석이라 정의하자.

이제 $\mathbb{v'}_{w_j}$를 $\mathbb{W}'$의 $j$-th row라 정의하고, j번째 word의 score를 $u_j$라 정의하면 $u_j=\mathbb{v'}_{w_j} \cdot \mathbb{h}$가 된다.

마지막으로 Probability를 구하기 위해 $softmax(u_j)$를 $y_j$로 정의한다.

이제

• $\mathbb{v}_w$: input vector
  • $W$의 column
• $\mathbb{v’}_w$: output vector
  • $W’$의 row

라고 부른다.

Backpropagation

Output -> Hidden layer

$o$가 true word의 index일 때 업데이트는 다음처럼 이루어진다.

해석:

• j = o인 경우
  • $\mathbb{v’}_{w_j}$를 $\mathbb{h}$에 가깝게 update한다. 그런데 $\mathbb{h}$는 input vector repr.이니까 input vector에 가깝게 간다고 볼 수 있다.
• j != o인 경우
  • $\mathbb{v’}_{w_j}$를 $\mathbb{h}$에서 멀어지도록 update한다.

label이 o일 때 backpropagation 계산…
$L = -log\left ( \frac{exp(u_o)}{\sum exp(u_{j})} \right )$
$\frac{\partial L}{\partial u_j} = softmax(u_j) - \mathbb{1}(j = o) := e_j$
$u_j = \mathbb{W'}_{ (j, :) } \cdot \mathbb{h} = \sum w'_{j,i} \cdot h_i$ 니까
$\frac{\partial L}{\partial w'_{j,i}} = \frac{\partial L}{\partial u_j} \cdot \frac{\partial u_j}{\partial w'_{j,i}} = e_j \cdot h_i$

Hidden -> Input layer

해석:

• input vector와 관련있는 column 하나만…
  • input vector는 output vector에 가까워지며, 나머지 vector에 대해서 error term만큼 멀어진다.
• otherwise
  • 그대로.

label이 o일 때 backpropagation 계산… (계속)
$\frac{\partial \mathbb{u}}{\partial \mathbb{h}} = \mathbb{W}'$
$\frac{\partial u_j}{\partial h_i} = w'_{j,i}$이므로
$\frac{\partial L}{\partial h_i} = \sum_{j=1}^{V}\frac{\partial L}{\partial u_j} \cdot \frac{\partial u_j}{\partial h_i}=\sum_{j=1}^{V}e_j \cdot w'_{j,i} := {EH}_i$
$EH$ : 모든 output vector의 summation인데, 단어의 prediction error로 weighted된 것!
-> 맞는 output vector는 +, 아닌 output vector는 -를 해서 더해준 녀석.
$h_i = \sum w_{i,k} \cdot x_k$이므로
$\frac{\partial L}{\partial w_{i,k}} = \frac{\partial L}{\partial h_i} \cdot \frac{\partial h_i}{\partial w_{i,k}} = {EH}_i \cdot x_k$

Multi-word context

이제는 여러 단어를 보는 CBOW 모델을 살펴보자. 아까처럼 바로 input-vector를 hidden으로 가져오는 것이 아니라, 평균을 내서 쓴다. 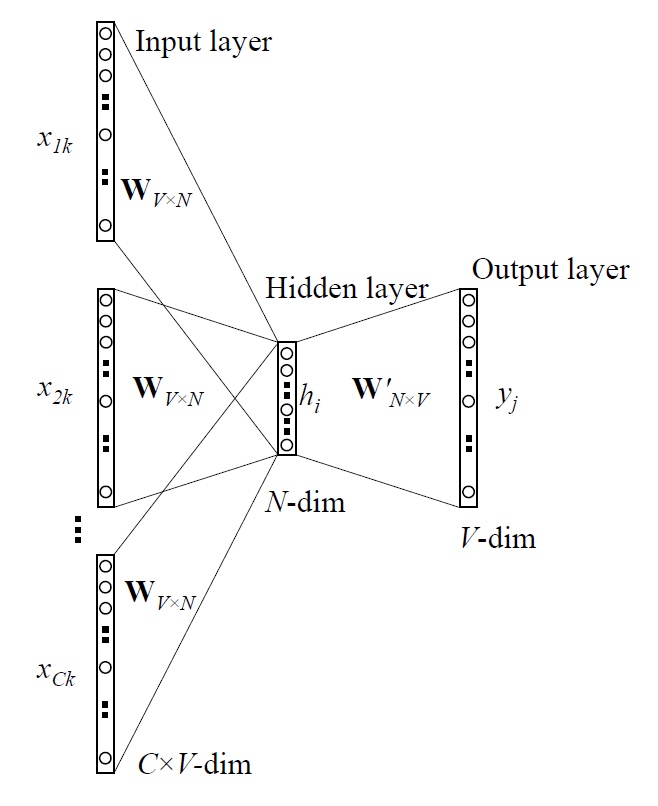$\mathbb{h} = \frac{1}{C}\mathbb{W}(\mathbb{x_1}+ ... + \mathbb{x_C})$ 요렇게 만들면 Hidden까지의 Backpropagation은 똑같다.

$\mathbb{v'}^{(new)}_{w_j} = \mathbb{v'}^{(old)}_{w_j} - \eta\cdot (y_j - \mathbb{1}(j = o)) \cdot \mathbb{h}$ 의미는 역시 제대로 예측된 녀석은 평균 input vector에 가까워지고, 아닌 녀석은 멀어지게 한다는 것!

Hidden -> Input layer

$\mathbb{v}^{(new)}_{w_{I,c}} = \mathbb{v}^{(old)}_{w_{I,c}} - \frac{1}{C} \cdot \eta\cdot {EH}^T$ 이것도 똑같이 업데이트하는데, $\frac{1}{C}$로 나눠서 가까워지고 멀어진다는 것!

Skip-gram Model

input 1개로 여러개의 단어를 유추한다. 여기서는 softmax가 N개가 나오겠지?

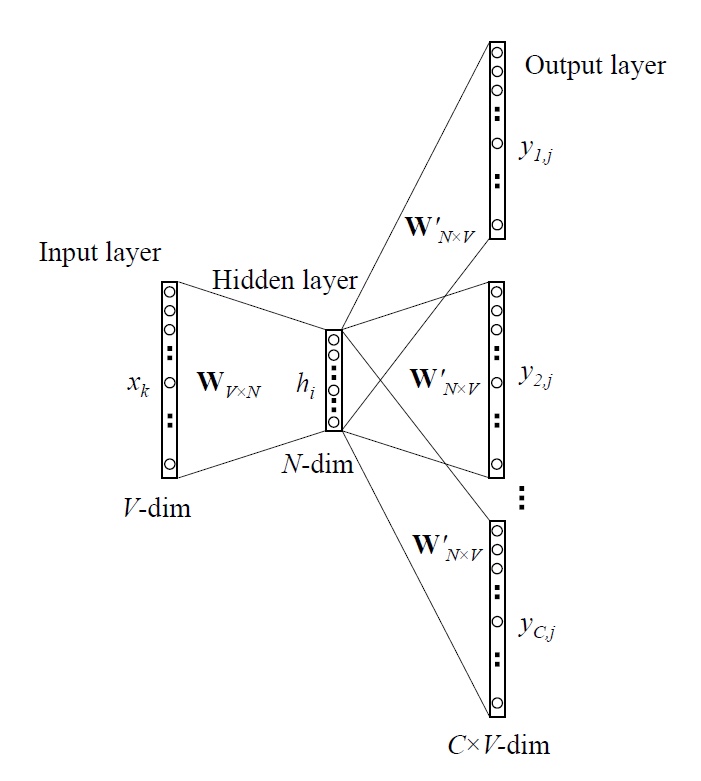
Backpropagation

Output -> Hidden layer

${EI}_j = \sum_{c=1}^C(y_{j,c} - \mathbb{1}(j_c = o_c))$ 로 정의하면
$\mathbb{v'}^{(new)}_{w_j} = \mathbb{v'}^{(old)}_{w_j} - \eta\cdot {EI}_j \cdot \mathbb{h}$

Hidden -> Input layer

${EH}_i = \sum_{ j=1 }^V {EI}_j \cdot w'_{j,i}$로 정의하면 CBOW의 식과 같아진다.

계산 복잡도 줄이기!

Hierarchical Softmax

$p(w = w_O) = \Pi_{j=1}^{L(w)-1}\sigma\left ( [n(w,j+1) = ch(n(w,j))]\cdot \mathbb{v'}_{n(w,j)}\cdot \mathbb{h} \right )$

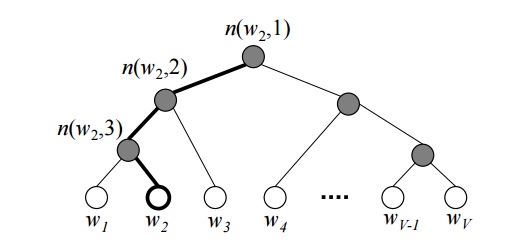
• n(w,j) : 단어 w의 j번째 unit
• ch(n) : n의 왼쪽 자식노드
• $v’_{n(w,j)}$ : inner unit n(w,j)의 output vector
• $W’$안쓴다.
  • 대신 V-1개의 inner-node들이 output vector $v’_{n(w,j)}$를 가진다.
• $\mathbb{[}x\mathbb{]}$ : x가 참이면 1, 거짓이면 -1

위의 예제에서 root node는 단 두개의 vector repr.만 가지면 되며, 업데이트할 때에도 자기 vector repr.만 신경쓰는 듯! $v'_{n(w_{1:3},1)}$ $v'_{n(w_{4:V},1)}$

Negative Sampling

motivation

softmax를 전체에 대해서 해버리니 너무 계산량이 많다. 여기서 sample을 뽑아서 얘네만 update하는건 어때?

방법

일단 ground truth는 당연히 들어가야하고(positive sampling), negative sample들을 몇 개 뽑아서 같이 update해야한다.(그래서 이름이 이렇게…)

• $P_n(w)$ :noise distribution
  • sample을 draw할 distribution
  • 임의로 고를 수 있다.

    unigram distribution의 3/4승 한게 제일 좋다더라.. $P_n(w_i)= \frac{ f(w_i)^{3/4} }{ \sum_{j=0}^n f(w_j)^{3/4} }$

loss를 요렇게 계산한게 좋다더라. $L = -log\sigma(\mathbb{v'}_{w_o}\mathbb{h}) - \sum_{w_j \in \dot{W}_{neg}}log\sigma(-\mathbb{v'}_{w_j}\mathbb{h})$

• $\dot{W}_{neg}$ : negative sampling한 녀석의 set