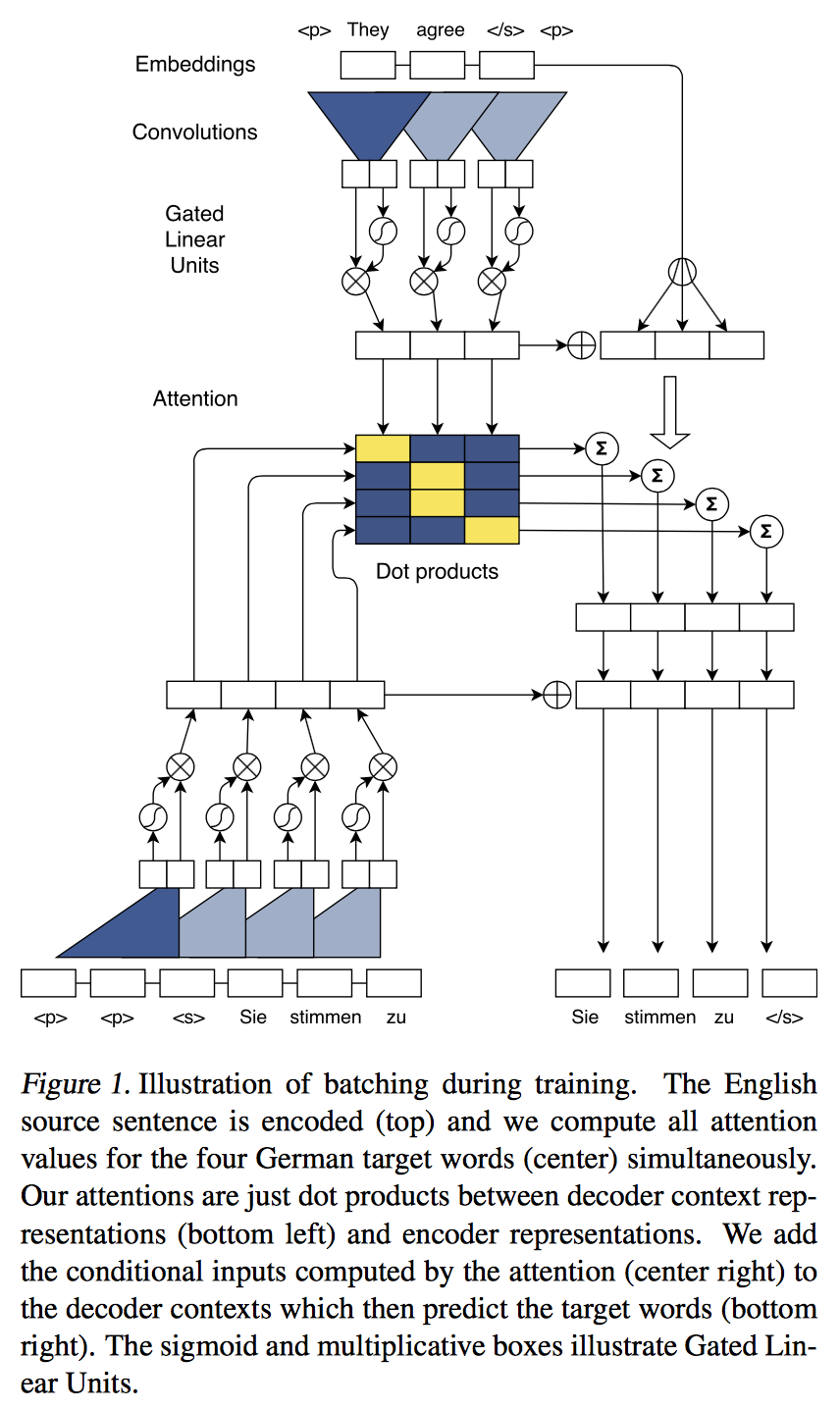
Convolutional Sequence to Sequence Learning 정리
13 Jun 2017 | ml nmt사실 이 논문을 보다가 구글에서 나온 transformer때문에 모두 정리하지는 못했다…
Abstract
training 시에 전부 parallelize!
2. Recurrent Sequence to Sequence Learning
여기서는 기존의 RNN을 사용한 seq2seq structure를 간단히 다룬다.
Overview
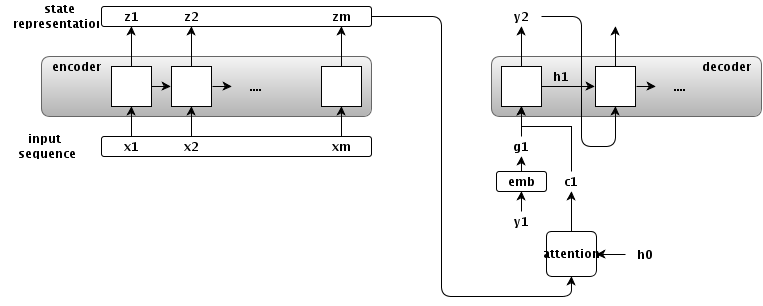 정확하게는 $h_0$ -> $h_1$으로 바꾸는게 맞겠다… 감안하고 보자!
정확하게는 $h_0$ -> $h_1$으로 바꾸는게 맞겠다… 감안하고 보자!
encoder
- input sequence
- $\textbf{x} = (x_1, …, x_m)$
- state representations
- $\textbf{z} = (z1, …, z_m)$
- input time-step : $m$
attention
- conditional input(attention output)
- $c_i = f(\textbf{z}, h_i)$
- 의미 : 각 time-step의 state representation과 $i$번째 decoder의 state의 함수로 conditional output을 만들겠다.
- attention을 쓰지 않는 seq2seq 모델의 일반화
- $c_i = z_m$ for all $i$
- 그냥 맨 마지막 state를 계속 넣겠다.
- $c_i = None$, $h_0 = z_m$
- encoder의 마지막 state를 decoder의 첫 input으로..
- $c_i = z_m$ for all $i$
decoder
- output sequence
- $\textbf{y}=(y_1, …, y_n)$
- hidden state
- $h_i$ : decoder의 $i$번째 hidden state
- embedding
- $g_i$ : $y_i$의 embedding.
- $y_{i+1}$을 만들려면…
- $h_{i+1}$을 만들어야함
- $h_i$ 가져오고
- $y_i$로 $g_i$를 만들고,
- $\textbf{z}$로 $c_i$를 만든다.
- 위 세개로 $h_{i+1}$을 만든다.
- 그 후엔 쉽지…
- $h_{i+1}$을 만들어야함
3. A Convolutional Architecture
이제 논문에서 주장하는 $\textbf{h}, \textbf{z}$를 CNN으로 계산하는 방법으로 넘어가보자!
3.1 Position Embeddings
- embedding matrix $\textbf{D}$
- $\textbf{D} \in \textbf{R}^{V \times f}$
- 변환: $\textbf{x} = (x_1,…,x_m)$ -> $\textbf{w}=(w_1, …, w_m)$
- $w_j \in \textbf{R}^{f}$ 는 $\textbf{D}$의 한 row
- absolute position embedding $\textbf{p}$
- $\textbf{p}=(p_1, …, p_m)$
- $p_j \in \textbf{R}^{f}$
- input element representation $\textbf{e}$
- 위 두개를 사용함
- $\textbf{e}=(w_1+p_1, …, w_m+p_m)$
absolute position embedding에 관한 내용이 제대로 안나와있다… 나중에 추가해야할 듯!
3.2 Convolutional Block Structure
- encoder와 decoder는 서로 block structure를 공유한다.
- 고정된 사이즈의 input element들로 중간 state들을 계산.
- $l$번째 block을 다음처럼 표기함
- encoder network : $\textbf{z}^l\ =\ (z^l_1,\ …,\ z^l_m)$
- decoder network : $\textbf{h}^l\ =\ (h^l_1,\ …,\ h^l_n)$
- 하나의 block은 1D의 convolution + non-linear func로 이루어짐
- block을 쌓으면 state가 표현하는 input element의 갯수가 증가
- 6개를 쌓으면 25개의 input을 하나의 state로 나타냄
- (5->9->13->17->21->25)
- 6개를 쌓으면 25개의 input을 하나의 state로 나타냄
Block
- convolutional kernel
- parameters
- $W \in \textbf{R}^{2d \times kd}$
- $b_w \in \textbf{R}^{k \times d}$
- input
- $X \in \textbf{R}^{k \times d}$
- $d$ 사이즈로 embedding된 $k$개의 input
- output
- $Y \in \textbf{R}^{2d}$
- parameters
- GLU(Gated Linear Unit)
- $\nu([A\ B]) = A * \sigma(B)$
- 그래서 결국 $R^d$
- Residual connection
- conv 결과 + residual conn