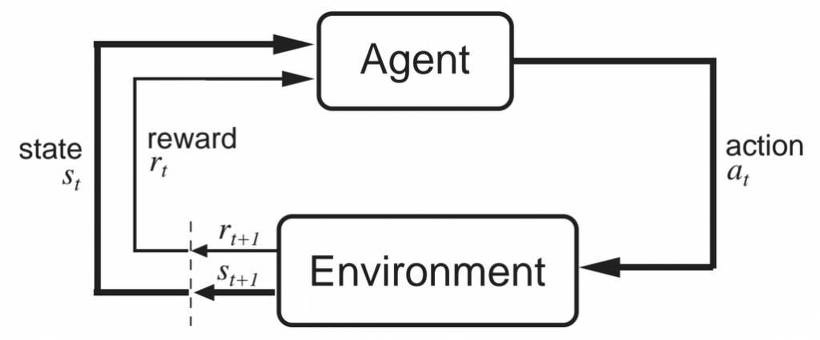
RL ch 2. MDP, Bellman Equation
12 Mar 2018 | ml rl bellman equation MDP2장 - 강화학습 기초 1: MDP와 벨만 방정식
MDP
- 순차적 행동 결정 문제를 수학적으로 정의
- 다음 6가지로 구성
- state
- agent가 관찰 가능한 상태의 집합(S)
- $S ={(x_1,y_1),(x_2, y_2),…}$
- action
- agent가 할 수 있는 가능한 행동의 집합(A)
- $A_t = a$ : t-step에 a라는 action을 취함
- reward
- 환경이 agent에게 주는 정보
- $R_s^a = E[R_{t+1} \vert S_t=s,A_t=a]$
- t-step에 상태가 s, 행동이 a일 때, 환경이 주는 보상의 기대값
- 환경에 대해서 sampling
- state transition probability
- 같은 action을 취해도, 다음 state는 다를 수 있다.
- $P_{ss’}^a = P[S_{t+1}=s’ \vert S_t=s,A_t=a]$
- discount factor
- 먼 미래의 보상을 현재의 가치로 따질 때 필요
- policy
- 어떤 state에서 agent가 할 action
- $\pi(a \vert s) = P[A_t=a \vert S_t=s]$
- state
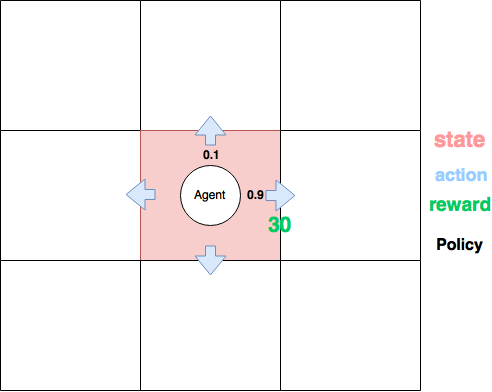
학습방법
- agent는 환경으로부터, 상태($s_t$)와 보상($r_t$)를 받고, 자신의 policy($\pi$)에 따라 행동($a_t$)을 함
- 환경은 행동($a_t$)에 대해 새로운 상태와 보상을 주고, agent는 보상을 최대화하는 방향으로 학습
Value function(가치함수)
- Value function은 다음 두 가지가 존재 (보통 앞의 것을 value func라 하지만..)
- State-value function - 상태의 가치
- Action-value function(Q-function) - 상태 + 행동의 가치
State-value function
- 먼저 return을 정의하자
- $G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}…$
- 에피소드가 끝난 이후 보상들을 정산할 때 필요
- 이제 value function을 정의하면
- $v(s)=E[G_t \vert S_t=s]$
- 어떤 상태에 있을 때의 앞으로 보상을 얼마나 받을 수 있을까
- recursive하게 정의하면
- $v(s) = E[R_{t+1}+\gamma v(S_{t+1}) \vert S_t=s]$
- 사실 MDP에서 action을 취해야 다음 state로 가기 때문에, policy가 빠질 수 없다.
- $v_\pi(s) = E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1}) \vert S_t=s]$
- 요게 Bellman Expectation Equation!! 뒤에 나옴
Action-value function (Q-function)
- 상태 + 행동에 대한 가치를 매김
- $q_\pi(s,a) = E_\pi[R_{t+1} + \gamma q_\pi(S_{t+1},A_{t+1}) \vert S_t=s, A_t=a]$
위 두 함수의 관계: $v_\pi(s) = \sum_{a\in A} \pi(a \vert s) q_\pi(s,a)$
Bellman Equation
- Dynamic programming으로 문제를 풀기 전에 Bellman Equation을 정리해보자!
- Bellman Expectation Equation
- $v_\pi(s) = E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1}) \vert S_t=s]$
- $v_\pi(s) = \underset{a \in A}{\Sigma}\pi(a\vert s)[R_{t+1} + \gamma \underset{s’ \in S}{\Sigma}P_{ss’}^av_\pi(s’)]$
- 별거 아니고, policy와 STP를 고려해서 계산한 것
- 이 걸 찾는다는 것 -> policy $\pi$에 대해 state $s$의 value-function을 찾은 것!
- Bellman Optimality Equation
- optimal value-function
- $v^*(s) = \underset{\pi}{max}[v_\pi(s)]$
- $v_\pi(s)$중 현재 state의 가치를 최대화하는 policy를 찾아내는 것!
- optimal Q-function
- $q^*(s,a)=\underset{\pi}{max}[q_\pi(s, a)]$
- 여기까지 구했으면 최적 정책을 만드는 것은 쉽다.
- optimal value-function