3장 - 강화학습 기초 2: Grid world & Dynamic programming

• 앞서서 MDP를 정의하고, Bellman 방정식들을 봤음
• dynamic programming을 통해서 최적 가치함수와, 최적 정책을 구하는 것이 이 장의 목적
• 다음 두가지 방법을 배움
  • Policy iteration
    • Bellman expectation eq. 을 사용
  • Value iteration
    • Bellman optimality eq.를 사용
• 쉽게 설명하기 위해 Grid world 예제를 사용하고, state transition probability는 무시한다.

Policy iteration

• 다음 세단계로 이루어짐
  • policy 초기화
  • policy evaluation
    • review
      • BEE: $v_\pi(s) = \underset{a \in A}{\Sigma}\pi(a \vert s)(R_{t+1} + \gamma v_\pi(s’))$
    • 위 수식을 iteration을 돌면서 구해본다
    • $v_{k+1}(s) = \underset{a \in A}{\Sigma}\pi(a \vert s)(R_{t+1} + \gamma v_k(s’))$
    • 
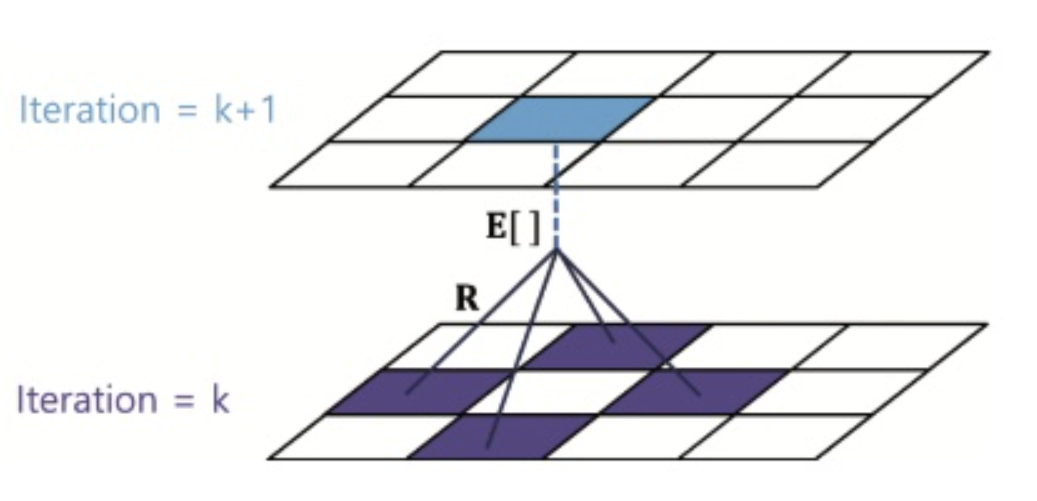
    • 이걸 모든 상태 s에 대해 수행
  • policy improvement
    • 여러가지 가능하나 Greedy Improvement를 소개한다.
    • review
      • q-func: $q_\pi(s,a) = E_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) \vert S_t=s, A_t=a]$
    • $q_\pi(s,a) = R_{s}^a + \gamma v_\pi(s’)$ 로 고침
    • 위 식을 최대화하는 action a를 반환하는 정책
• policy와 value-function이 분리되어있음
  • 확률적 policy도 가능하다.

Value iteration

• value function에 대해서 최적의 value func.만 뽑는 정책을 가정함
• 이러면 val. func.에 policy그 내재됨
• v(s)만 잘 업데이트하면 되겠다!
• review
  • BOE: $v^*(s) = \underset{a}{max} E[R_{t+1}+\gamma v^*(S_{t+1}) \vert S_t=s, A_t=a]$
• 요걸 똑같이 update하는 식으로 만들면
  • $v_{k+1}(s) = \underset{a \in A}{max}[R_s^a+\gamma v_k(s’)]$
• 

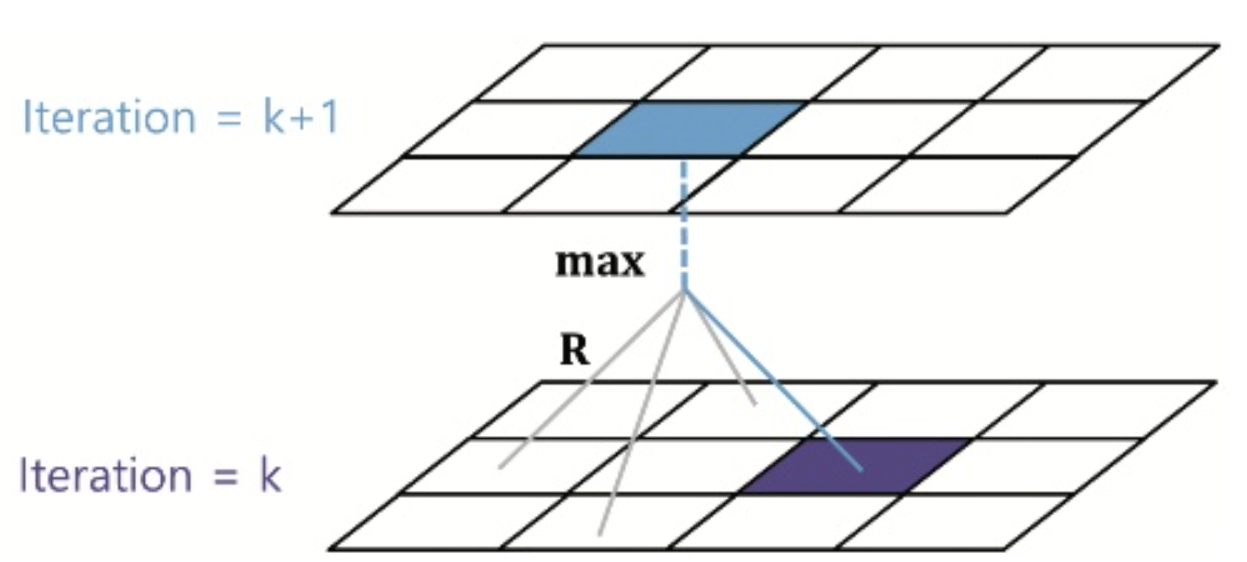
DP의 한계

• 계산 복잡도 및 curse of Dim.
• 환경에 대한 완벽한 정보가 필요!!