강화학습 기초 3: Grid world & Q-learning

• RL은 환경의 모델을 몰라도 상호작용을 통해 학습이 가능

• DP는 환경의 모델을 알아야함

• 예측: policy가 주어졌을 때, Value func.를 계산하는 것(evaluation)
  • 몬테카를로 예측
  • 시간차 예측
• 제어: Value func.를 토대로 agent의 optimal policy를 찾는 것(Improvement)
  • Sarsa (시간차 제어)
  • Q-learning (off-policy)

강화학습과 정책 평가 1: Monte-carlo prediction(MC)

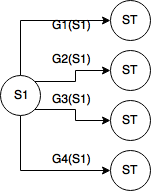ST: terminal state, Gi: i번째 episode의 return

• DP에서는 모든 state에 대해서 동시에 update를 함
• review (B.E.E.)
  • $v_\pi(s) = E_\pi[R_{t+1} + \gamma v_\pi(s’)]$
• Sampling을 통해서 $v_\pi$를 구해보자!
  • $$\begin{matrix} v_\pi(s) & = & E[ R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}... \vert S_t=s] \\ & = & E[G_t \vert S_t=s] \end{matrix}$$
  • 끝까지 episode를 진행시켜서 $G_t$를 얻어냄
  • 그 $G_t$들을 평균내서 쓰겠다
  • $$v_\pi(s) = \frac{1}{N(s)}\underset{i=1}{\overset{N(s)}{\Sigma}}G_i(s)$$
• sample update(n개의 sample이 있을 때, n+1번째 sample이 들어옴)
  • $$\begin{matrix}V_{n+1} & = & \frac{1}{n}\Sigma_i^{n}G_i\\ & = & \frac{1}{n}(G_{n}+\Sigma_i^{n-1}G_i) \\ & = & \frac{1}{n}(G_{n} + (n-1) * \frac{1}{n-1}\Sigma_i^{n-1}G_i) \\ & = & \frac{1}{n}(G_{n} + (n-1)V_n) \\ & = & V_n + \frac{1}{n}(G_{n}-V_{n})\end{matrix}$$
• 일반 업데이트 식
  • $V(s) \leftarrow V(s) + \alpha(G(s) - V(s))$
  • $G(s)$에 다가가도록 step-size($\alpha$)만큼 update
• 장점
  • 각 state에 independent하다
    • DP에서는 인접 state에 대해서 구했는데…
    • $V(s) \leftarrow V(s) + \alpha(G(s) - V(s))$로 끝남
  • 전체 state가 아닌 특정 state에 대해서만 구해도 된다.
• 단점
  • 모든 state를 가보지 못했는데, guarantee할 수 있나?
    • 주어진 정책대로 간다면 갈 확률이 거의 없으니 괜찮음…
  • episode가 끝나야지 update를 할 수 있네????
    • episode가 끝나지 않는 문제에는 적용 못함 ㅠ
    • temporal diff로 가자!

강화학습과 정책 평가 2: Temporal difference(TD)

• Monte-carlo의 수식을 다시 살펴보자
  • $V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))$
  • $G_t$는 episode가 끝나야 알 수 있다.
• $G_t = R_{t+1} + \gamma v_\pi(s’)$
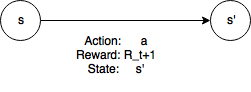
• episode의 중간 상태에서(s) 액션(a)를 취하면 다음 상태(s’)과 보상 $R_{t+1}$을 알 수 있다.
• 현재의 보상 $R_{t+1}$에 예측한 value func. $V(s’)$을 $G_t$대신 쓰는 것이 Temporal difference!!

비교

• MC : high variance, zero bias
• TD : low variance, some bias
  • 하지만 MC보다 효율적이고, 더 빨리 수렴한다.
  • 초기값에 sensitive(bootstrap)

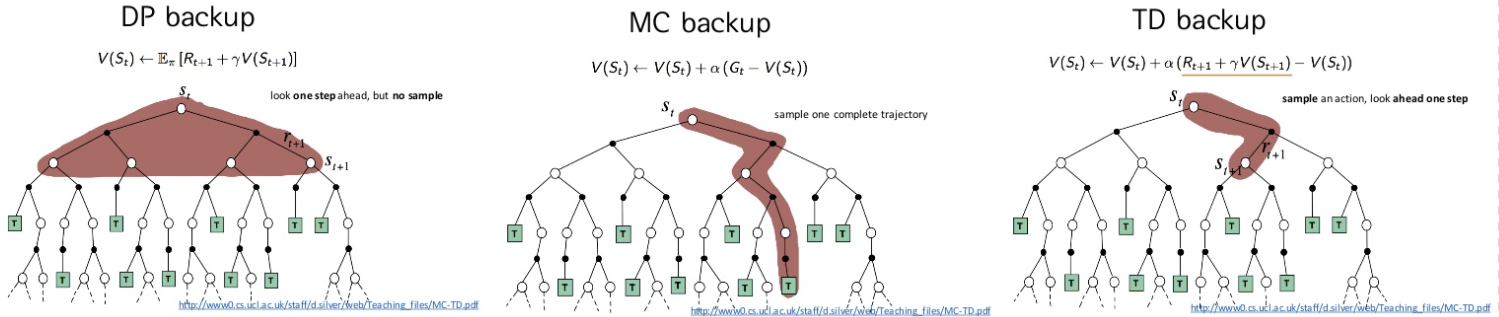
사실 위의 TD는 TD(0)며, TD(n)의 경우 n스텝을 더 본 이후 $G_t$를 예측한다.

강화학습 알고리즘 1: Sarsa

• GPI(Generalized Policy Iteration)
  • policy iteration인데, evaluation / improvement를 한번씩 번갈아가며 진행
  • 이렇게 해도 수렴이 된다네…
• Sarsa
  • policy evaluation: Temporal difference
  • policy improvement
    • Greedy policy
      • $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha(R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) )$
      • 
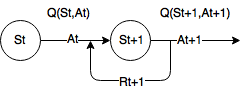
      • $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$가 학습에 필요!
    • $\epsilon$-greedy
      • 위 식에서 action들은 greedy policy를 따른다면, Q-func의 초기값에 지배됨!
      • 그래서 어느정도는 탐험이 필요함
      • $$\pi(s) = \left\{\begin{matrix}a^*=\underset{a\in A}{argmax}Q(s,a), & 1-\epsilon\\ a \neq a^* & \epsilon \end{matrix}\right.$$
  • 정리
    • $\epsilon$-greedy 방식으로 sample $(S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1})$ 를 얻어냄
    • 이 샘플로 $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha(R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) )$를 계산하고 update

강화학습 알고리즘 2: Q-learning

• Sarsa의 한계
  • 
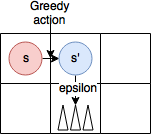
  • 다음 state의 action이 탐험에 의해서 잘못된 선택을 할 경우, 좋은 action이 penalty를 받는다.
  • $Q(s’,a’)$가 작기 때문에…
  • on-policy temporal difference control
    • 자신이 행동하는대로 학습하는 시간차 제어
• Q-learning
  • off-policy TD control
    • 행동하는 정책
    • 학습하는 정책
    • 을 따로 가져가자!
  • $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha(R_{t+1} + \gamma \underset{a’}{max}Q(S_{t+1}, a’) - Q(S_t, A_t) )$
    • 다음 state의 action을 greedy로
      • 학습할 것은 $\epsilon$-greedy지만,
      • 그 안에서 가져오는 것은 greedy로 가정
    • $(S_t, A_t, R_{t+1}, S_{t+1})$ 가 필요