GPyOpt - Bayesian Optimization and tensorflow 예제 만들기

17 Oct 2017 | tensorflow bayesian inference optimization

문서 내용

여기서는 GPyOpt와 tensorflow를 사용하여, ML Model의 parameter를 최적화하는 실험을 한다.

Data: MNIST
Model: FNN Model
- input: 784-dim
- output: 10-dim
- parameter
  - learning-rate (0.01, 0.5)
  - layer 수 {2, 3}
  - hidden_size {30, 60}
  - batch_size {500, 1000, 2000}

tensorflow model with score

여기서는 먼저 tensorflow model을 만든다. Bayesian Optimization는 model을 학습하고 결과를 받는 함수를 objective function으로 생각하기 때문에 accuracy에 -를 취해주어야 한다.

TODO: Objective function의 scale에 따라서 다르게 최적화가 되는지… 알아봐야할 듯!

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('../MNIST_data', one_hot=True)

Extracting ../MNIST_data/train-images-idx3-ubyte.gz
Extracting ../MNIST_data/train-labels-idx1-ubyte.gz
Extracting ../MNIST_data/t10k-images-idx3-ubyte.gz
Extracting ../MNIST_data/t10k-labels-idx1-ubyte.gz

def objective_function(args):
    '''
    args[0] : layer 개수
    args[1] : hidden size
    '''
    lr_rate = args[0, 0]
    num_layer = args[0, 1].astype(int)
    output_size = args[0, 2].astype(int)
    batch_size = args[0, 3].astype(int)

    
    print("실험 시작\nargs: {}".format(args))
    # reset graph
    tf.reset_default_graph()
    
    x = tf.placeholder(tf.float32, shape=[None, 784])
    y_ = tf.placeholder(tf.float32, shape=[None, 10])
    
    input_size = 784
    remain_num_layer = num_layer-1
    
    new_x = x  # feed_dict에 x로 들어가기 위해서...
    for i in range(remain_num_layer):
        W = tf.Variable(tf.random_normal([input_size, output_size]))
        b = tf.Variable(tf.random_normal([output_size]))
        new_x = tf.nn.relu(tf.matmul(new_x, W) + b)
        input_size = output_size

    W = tf.Variable(tf.random_normal([input_size, 10]))
    b = tf.Variable(tf.random_normal([10]))
    
    y = tf.matmul(new_x, W) + b
    cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_,
                                                                           logits=y))

    global_step = tf.Variable(0, trainable=False)

    lr_rate_decayed = tf.train.exponential_decay(lr_rate,
                                                 global_step,
                                                 10,
                                                 0.99,
                                                 staircase=True)
    train_step = tf.train.GradientDescentOptimizer(lr_rate_decayed).minimize(cross_entropy)

    acc = [0]
    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())

        for i in range(1000):
            batch = mnist.train.next_batch(batch_size)
            train_step.run(feed_dict={x: batch[0], y_: batch[1]})

            correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
            accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
            if i % 50 is 0:
                new_acc = accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels})
                print("중간 결과: {}".format(new_acc))
                if abs(new_acc - acc[-1]) < 0.0001: #효과가 별로 없으면
                    break
                else:
                    acc.append(new_acc)
                
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
        
        acc = accuracy.eval(feed_dict={x : mnist.test.images,
                                       y_: mnist.test.labels})
        print("실험 하나 종료! 결과\nargs: {}, acc: {}".format(args, acc))
        return 1 - acc  # fMin이기 때문에...

Bayesian Optimization

위 코드 마지막을 보면 1-acc로 accuracy에 마이너스를 취해줬지..

이제 다음 코드로 Bayesian Optimization을 하면 끝!

from GPyOpt.methods import BayesianOptimization
import numpy as np

# continuous가 discrete 앞에 위치해야함! BUGBUG!! https://github.com/SheffieldML/GPyOpt/issues/85
domain = [{'name': 'lr_rate',
          'type': 'continuous',
          'domain': (0.01, 0.5),
           'dimensionality': 1},
          {'name': 'num layer',
           'type': 'discrete',
           'domain':(2, 3),
           'dimensionality': 1},
          {'name': 'hidden size',
           'type': 'discrete',
           'domain': (30, 60),
           'dimensionality': 1},
          {'name': 'batch size',
           'type': 'discrete',
           'domain': (500, 1000, 2000),
           'dimensionality': 1}]

# --- Solve your problem
myBopt = BayesianOptimization(f=objective_function,
                              domain=domain,
                              initial_design_numdata=5)
myBopt.run_optimization(max_iter=15)
myBopt.plot_acquisition()

실험 시작
args: [[  3.27519352e-01   3.00000000e+00   6.00000000e+01   1.00000000e+03]]
중간 결과: 0.11749999970197678
...
중간 결과: 0.8468000292778015
중간 결과: 0.8496000170707703
실험 하나 종료! 결과
args: [[   0.5    2.    30.   500. ]], acc: 0.8436999917030334

결과 보기

다음 코드로 결과를 확인할 수 있다.

print(myBopt.x_opt)  # lr_rate, #layer, hidden_size, batch_size

N, _ = myBopt.X.shape
for i in range(N):
    if np.array_equal(myBopt.x_opt, myBopt.X[i, :]):
        print(1 - myBopt.Y[i,:])  # accuracy 변환

[  2.72432763e-01   2.00000000e+00   6.00000000e+01   2.00000000e+03]
[ 0.87239999]

부록

# 돌릴 필요는 없고 참고삼아...
args = np.array([[2, 10, 500, 0.3]])
objective_function(args)

t-SNE

13 Oct 2017 | ml dimension reduction

이론적 배경

Stochastic Neighbor Embedding(SNE)

고차원 원공간에 존재하는 데이터 x의 이웃간의 거리를 최대한 보존하는 저차원의 y를 학습하는 방법론

원래의 고차원 공간에 존재하는 i번째 object가 주어졌을 때, j번째 object가 선택될 확률
- ${ p }_{ j\vert i }=\frac { { e }^{ -\frac { { \left\vert { x }_{ i }-{ x }_{ j } \right\vert }^{ 2 } }{ 2{ \sigma }_{ i }^{ 2 } } } }{ \sum _{ k }^{ }{ { e }^{ -\frac { { \left\vert { x }_{ i }-{ x }_{ k } \right\vert }^{ 2 } }{ 2{ \sigma }_{ i }^{ 2 } } } } }$
저차원의 공간에서 i번째 object가 주어졌을 때, j번째 object가 선택될 확률
- ${ q }_{ j\vert i }=\frac { { e }^{ -{ \left\vert { y }_{ i }-{ y }_{ j } \right\vert }^{ 2 } } }{ \sum _{ k }^{ }{ { e }^{ -{ \left\vert { y }_{ i }-{ y }_{ k } \right\vert }^{ 2 } } } }$

SNE는 위 두 확률이 비슷해지면 저차원이 잘 모델링된다고 가정을 한다. 확률의 비슷함은 당연히 KL divergence!

그래서 다음 식을 최소화시키도록 학습을 한다. $\begin{align*} Cost&=\sum _{ i }^{ }{ KL({ P }_{ i }\vert \vert { Q }_{ i }) } \\ &=\sum _{ i }^{ }{ \sum _{ j }^{ }{ { p }_{ j\vert i }\log { \frac { { p }_{ j\vert i } }{ { q }_{ j\vert i } } } } } \end{align*}$

t-SNE

SNE에서 $\sigma_i$는 원래 dense한 곳에서는 작고, sparse한 곳에서는 크게 하려고 했는데, 상수로 고정하여도 성능에 큰 차이가 없었음.
$p_{i\vert j}$와 $p_{j\vert i}$를 같이 놓고 풀어도 성능이 그리 나쁘지 않았음.
- 그래서 요렇게 변경
  - ${ p }_{ ij }=\frac { { p }_{ j\vert i }+{ p }_{ i\vert j } }{ 2 } ,\quad { q }_{ ij }=\frac { { q }_{ j\vert i }+{ q }_{ i\vert j } }{ 2 }$
그래서 다시 계산하면
- $\begin{align*} Cost&=\sum _{ i }^{ }{ KL({ P }_{ i }\vert \vert { Q }_{ i }) } \\ &=\sum _{ i }^{ }{ \sum _{ j }^{ }{ { p }_{ ij }\log { \frac { { p }_{ ij } }{ { q }_{ ij } } } } } \\ \frac { \partial C }{ \partial { y }_{ i } } &=4\sum _{ j }^{ }{ ({ y }_{ j }-{ y }_{ i })({ p }_{ ij }-{ q }_{ ij }) } \end{align*}$
- 요리 나온다. 이거는 유도해보지 않았고… 어차피 gradient descent로 풀어버리니까…
gaussian은 꼬리가 얇아서 적당히 떨어진 것과 멀리 떨어진 것의 확률이 모두 작다.(crowding problem) 그래서 $q_{ij}$에 대해서 t-분포를 사용했음.
- ${ q }_{ ij }=\frac { { (1+{ \left\vert { y }_{ i }-{ y }_{ j } \right\vert }^{ 2 }) }^{ -1 } }{ \sum _{ k\neq l }^{ }{ { (1+{ \left\vert { y }_{ k }-{ y }_{ l } \right\vert }^{ 2 }) }^{ -1 } } }$

실제 쓸 때 필요한 정보

요거 쓰면 빠른데 dimension이 2일때만 된다…ㅠㅠ

multicore-TSNE 이 코드를 받아서 써야한다. scikit-learn의 t-sne와 여러 다른 t-sne 구현체에 대해서 [40164 x 512]로 실험했는데 다들 잘 안나온다. 심지어 segfault까지 나옴.. 요놈을 가져다 쓰자!

10분안에 끝남 (다른 녀석들은 몇시간 기다려도 안됨 ㅠ)

from MulticoreTSNE import MulticoreTSNE as TSNE
import numpy as np

def normalize_data(d):
    row_sums = d.sum(axis=1)
    return (d.T / row_sums).T

tsne = TSNE(n_jobs=16, metric="cosine")  # 16코어, cosine metric
emb = np.load("testKrEn/en_pair.npy")
emb2 = emb.astype(np.double)
Y = tsne.fit_transform(emb2)
np.save("out_2.npy", Y)
Y_norm = normalize_data(Y)
np.save("out_norm_2.npy", Y_norm)

http://techfly.top/2017/03/09/machine_learning_tensorflow_tsne_data_nonlinear_dimensionality_reduction/ 요거 보고 구현해봐야하나…ㅠㅠ

https://github.com/maestrojeong/t-SNE/blob/master/t-SNE.ipynb

Python Threading

01 Sep 2017 | python thread

threading

Object	Description
Thread	thread 객체
Lock	기본 lock 객체
RLock	재진입 가능한 lock 객체
Condition	다른 쓰레드의 신호를 기다리는 condition 변수 객체
Event	컨디션의 일반화 버젼
Semaphore	세마포어
BoundedSemaphore	초기값 이상으로 증가할 수 없는 세마포어
Timer	지정된 시간동안 대기하고 실행되는 thread
Barrier	thread가 계속 진행되려면 지정된 숫자의 thread가 해당 지점까지 도달해야함

Thread class

method/attribute	Description
`daemon`	daemon thread인지..
`__init__`	초기화
`start()`	thread 실행
`run()`	thread의 기능을 담당
`join(timeout=None)`	thread가 종료될 때까지 대기한다

예제

함수를 넘김

import threading
from time import sleep, ctime

loops = [3, 1]

def loop(nloop, nsec):
    print('start loop {} at: {}'.format(nloop, ctime()))
    sleep(nsec)
    print('loop {} at: {}'.format(nloop, ctime()))


def test() :
    print('starting at: {}'.format(ctime()))
    threads = []
    nloops = range(len(loops))

    for i in nloops:
        t = threading.Thread(target=loop,
                             args=(i, loops[i]))
        threads.append(t)

    # thread들을 모두 실행시킨다.
    for i in nloops:
        threads[i].start()

    # thread들을 모두 join
    for i in nloops:
        threads[i].join()

    print('all Done at: {}'.format(ctime()))

if  __name__ == '__main__' : 
   test()

결과 :

starting at: Fri Sep  1 17:06:49 2017
start loop 0 at: Fri Sep  1 17:06:49 2017
start loop 1 at: Fri Sep  1 17:06:49 2017
loop 1 at: Fri Sep  1 17:06:50 2017
loop 0 at: Fri Sep  1 17:06:52 2017
all Done at: Fri Sep  1 17:06:52 2017

상속을 통해서

import threading
from time import sleep, ctime

loops = [3,1]

class MyThread(threading.Thread):
    def __init__(self, args, name=''):
        threading.Thread.__init__(self, name=name)
        self.args = args

    def run (self):
        print('start loop: {} at: {}'.format(self.args[0], ctime()))
        sleep(self.args[1])
        print('done loop: {} at: {}'.format(self.args[0], ctime()))


def test() :
    print('starting at: {}'.format(ctime()))
    threads = []
    nloops = range(len(loops))

    for i in nloops:
        t = MyThread((i, loops[i]),
                     'loop')
        threads.append(t)

    for i in nloops:
        threads[i].start()

    for i in nloops:
        threads[i].join()

    print('all Done at: {}'.format(ctime()))

if  __name__ == '__main__' : 
   test()

결과 :

starting at: Fri Sep  1 17:14:36 2017
start loop: 0 at: Fri Sep  1 17:14:36 2017
start loop: 1 at: Fri Sep  1 17:14:36 2017
done loop: 1 at: Fri Sep  1 17:14:37 2017
done loop: 0 at: Fri Sep  1 17:14:39 2017
all Done at: Fri Sep  1 17:14:39 2017

Condition

Contition 객체를 사용하는 예제를 적는다. 여기서 with statement를 쓰는 것을 볼 수 있는데…

with some_lock:
    # do something...

는

some_lock.acquire()
try:
    # do something...
finally:
    some_lock.release()

과 동치라고 한다. python 3부터 그런가보다..

밑의 예제는 하나씩 notify를 하는 것을 만들어보았고 notify_all()로 한번에 끝낼 수도 있다.

import threading
import time
import logging

logging.basicConfig(level=logging.DEBUG,
                    format='(%(threadName)-9s) %(message)s')

def consumer(cv):
    logging.debug('start')
    with cv:
        logging.debug('waiting')
        cv.wait()
        logging.debug('consumed the resource')

def producer(cv):
    logging.debug('start')
    with cv:
        logging.debug('produce a resource')
        cv.notify()
    
    logging.debug('sleep 4 seconds')
    time.sleep(4)
    with cv:
        logging.debug('produce a resource')
        cv.notify()

if __name__ == '__main__':
    condition = threading.Condition()
    cs1 = threading.Thread(name='consumer1', target=consumer, args=(condition,))
    cs2 = threading.Thread(name='consumer2', target=consumer, args=(condition,))

    pd  = threading.Thread(name='producer',  target=producer, args=(condition,))

    cs1.start()
    cs2.start()
    time.sleep(1)
    pd.start()

결과 :

(consumer1) start
(consumer1) waiting
(consumer2) start
(consumer2) waiting
(producer ) start
(producer ) produce a resource
(producer ) sleep 4 seconds
(consumer1) consumed the resource
(producer ) produce a resource
(consumer2) consumed the resource

Layer Normalization

04 Jul 2017 | ml normalization

Layer Normalization

Introduction

Batch Normalization
- input statistics의 running average를 필요로함
- RNN의 경우 time-step마다 다른 statistics를 적용해야함
- distributed training에서는 minibatch가 너무 작아서 적용이 힘듬

Background

$a_i^l$: l번째 layer의 i번째 hidden unit
$w_i^l$: parameter
$b_i^l$: bias parameter

라고 하면

다음과 같이 수식화할 수 있다. $a_i^l = w_l^l h^l$

$h_i^{l+1}=f(a_i^l+b_i^l)$

문제점: 한 layer의 weight들에 대한 gradient는 전 layer의 output에 높게 관여된다. internal covariate shift: 그런데 전 layer의 output이 계속 distribution이 바뀌니까 트레이닝이 느리다. BN 설명 블로그

그래서 Batch-normalization에서는 위에서 말한 internal covariate shift를 줄이기 위해

batch에 대해서 각 dimension마다 mean, variance를 구하여 normalization하고 (각 dim은 independent하다고 가정)
linear transform을한다. (실제 independent하진 않을테니..)
그리고 linear transform도 같이 트레이닝

$\bar{a}_i^l=\frac{g_i^l}{\sigma_i^l}(a_i^l-\mu_i^l)$

근데 위에서 $\sigma$와 $\mu$는 batch의 distribution으로 근사시켜서 구하는데, 이는 실제 distribution과 다르다. 그래서 작은 batch보다는 큰 batch가 좋다.

Layer Normalization

hidden unit들에 대해서 mean과 variance를 구함
- $\mu^l = \frac{1}{H}\sum_{i=1}^H a_i^l$
- $\sigma^l = \sqrt{\frac{1}{H}\sum_{i=1}^H (a_i^l-\mu^l)^2}$
batch size에 관계없으므로
- training, test시에도 따로 구할 것이 없음
- RNN에도 좋음

Convolutional Sequence to Sequence Learning 정리

13 Jun 2017 | ml nmt

사실 이 논문을 보다가 구글에서 나온 transformer때문에 모두 정리하지는 못했다…

Abstract

training 시에 전부 parallelize!

2. Recurrent Sequence to Sequence Learning

여기서는 기존의 RNN을 사용한 seq2seq structure를 간단히 다룬다.

Overview

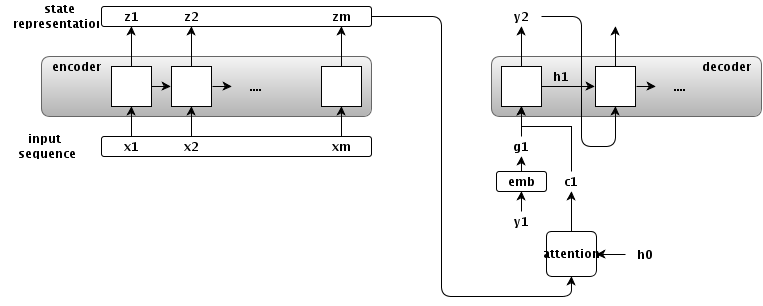정확하게는 $h_0$ -> $h_1$으로 바꾸는게 맞겠다… 감안하고 보자!

encoder

input sequence
- $\textbf{x} = (x_1, …, x_m)$
state representations
- $\textbf{z} = (z1, …, z_m)$
input time-step : $m$

attention

conditional input(attention output)
- $c_i = f(\textbf{z}, h_i)$
- 의미 : 각 time-step의 state representation과 $i$번째 decoder의 state의 함수로 conditional output을 만들겠다.
attention을 쓰지 않는 seq2seq 모델의 일반화
- $c_i = z_m$ for all $i$
  - 그냥 맨 마지막 state를 계속 넣겠다.
- $c_i = None$, $h_0 = z_m$
  - encoder의 마지막 state를 decoder의 첫 input으로..

decoder

output sequence
- $\textbf{y}=(y_1, …, y_n)$
hidden state
- $h_i$ : decoder의 $i$번째 hidden state
embedding
- $g_i$ : $y_i$의 embedding.
$y_{i+1}$을 만들려면…
- $h_{i+1}$을 만들어야함
  - $h_i$ 가져오고
  - $y_i$로 $g_i$를 만들고,
  - $\textbf{z}$로 $c_i$를 만든다.
  - 위 세개로 $h_{i+1}$을 만든다.
- 그 후엔 쉽지…

3. A Convolutional Architecture

이제 논문에서 주장하는 $\textbf{h}, \textbf{z}$를 CNN으로 계산하는 방법으로 넘어가보자!

3.1 Position Embeddings

embedding matrix $\textbf{D}$
- $\textbf{D} \in \textbf{R}^{V \times f}$
- 변환: $\textbf{x} = (x_1,…,x_m)$ -> $\textbf{w}=(w_1, …, w_m)$
  - $w_j \in \textbf{R}^{f}$ 는 $\textbf{D}$의 한 row
absolute position embedding $\textbf{p}$
- $\textbf{p}=(p_1, …, p_m)$
- $p_j \in \textbf{R}^{f}$
input element representation $\textbf{e}$
- 위 두개를 사용함
- $\textbf{e}=(w_1+p_1, …, w_m+p_m)$

absolute position embedding에 관한 내용이 제대로 안나와있다… 나중에 추가해야할 듯!

3.2 Convolutional Block Structure

encoder와 decoder는 서로 block structure를 공유한다.
- 고정된 사이즈의 input element들로 중간 state들을 계산.
$l$번째 block을 다음처럼 표기함
- encoder network : $\textbf{z}^l\ =\ (z^l_1,\ …,\ z^l_m)$
- decoder network : $\textbf{h}^l\ =\ (h^l_1,\ …,\ h^l_n)$
하나의 block은 1D의 convolution + non-linear func로 이루어짐
block을 쌓으면 state가 표현하는 input element의 갯수가 증가
- 6개를 쌓으면 25개의 input을 하나의 state로 나타냄
  - (5->9->13->17->21->25)

Block

convolutional kernel
- parameters
  - $W \in \textbf{R}^{2d \times kd}$
  - $b_w \in \textbf{R}^{k \times d}$
- input
  - $X \in \textbf{R}^{k \times d}$
  - $d$ 사이즈로 embedding된 $k$개의 input
- output
  - $Y \in \textbf{R}^{2d}$
GLU(Gated Linear Unit)
- $\nu([A\ B]) = A * \sigma(B)$
- 그래서 결국 $R^d$
Residual connection
- $h^l_i = \nu(W^l[h^{l-1}_{i-k/2},...,h^{l-1}_{i+k/2}] + b^l_w) + h^{l-1}_i$
- conv 결과 + residual conn

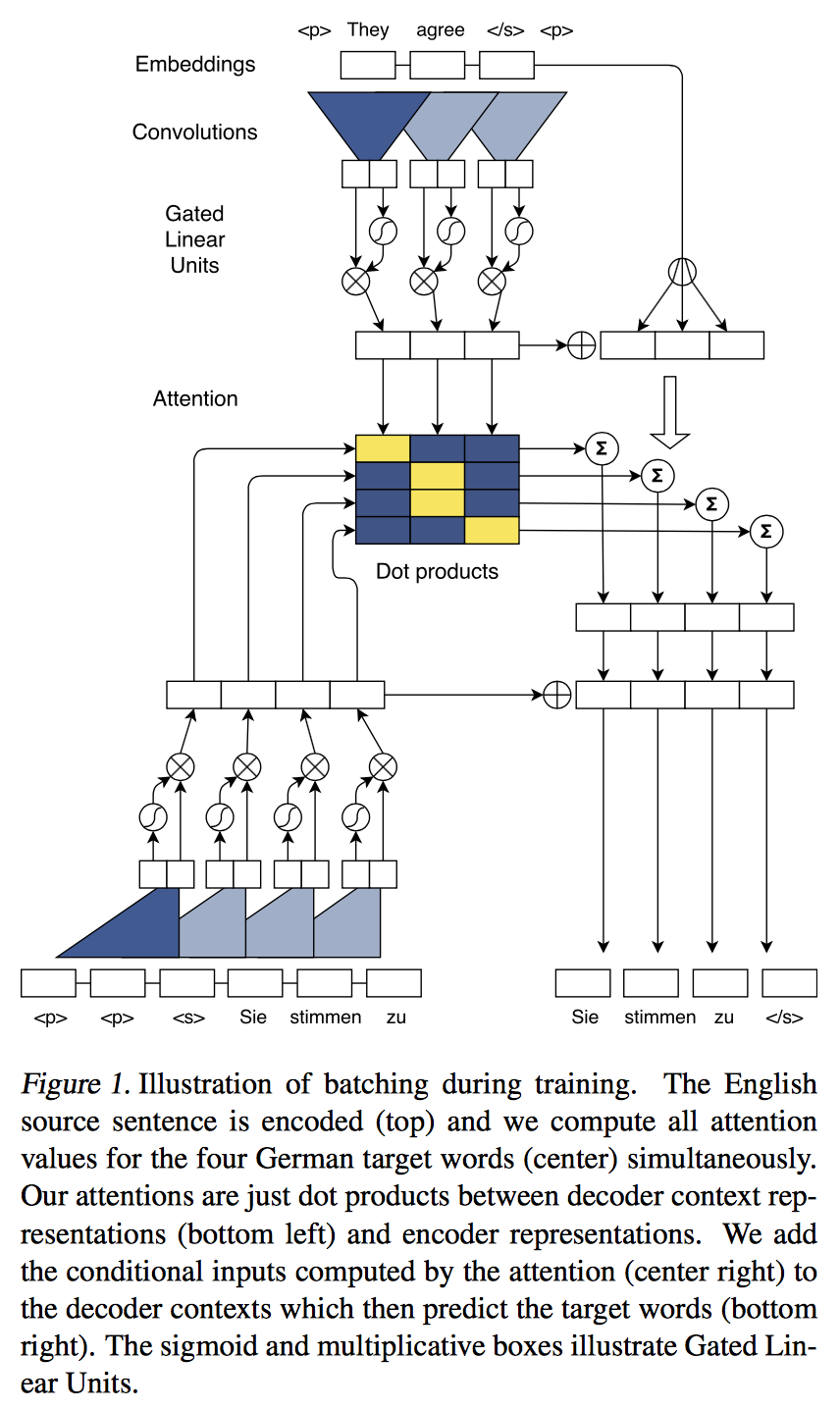
overview

Older Newer

Hulk의 개인 공부용 블로그

GPyOpt - Bayesian Optimization and tensorflow 예제 만들기

문서 내용

tensorflow model with score

Bayesian Optimization

결과 보기

부록

t-SNE

이론적 배경

Stochastic Neighbor Embedding(SNE)

t-SNE

실제 쓸 때 필요한 정보

Python Threading

threading

Thread class

예제

함수를 넘김

상속을 통해서

Condition

Layer Normalization

Layer Normalization

Introduction

Background

Layer Normalization

Convolutional Sequence to Sequence Learning 정리

Abstract

2. Recurrent Sequence to Sequence Learning

Overview

encoder

attention

decoder

3. A Convolutional Architecture

3.1 Position Embeddings

3.2 Convolutional Block Structure

Block