BLEU의 모든 것
05 Jun 2017 | ml nmt bleu metric참고문헌
BLEU
BLEU (bilingual evaluation understudy)는 기계번역을 통해 만들어진 text의 퀄리티를 evaluate하는 algorithm이다.
퀄리티는 기계번역의 output과 사람번역의 output을 비교하여 정해진다.
BLEU는 사람이 정하는 quality와 가장 높은 연관도를 보이는 첫 metric이며, 계산량도 많지 않기때문에, 지금도 많이 쓰인다.
score는 각 문장에 대해서 reference와 비교하여 계산되고, 이를 전체 corpus에 대해 average한다.
실제로는,
(전체 corpus의 n-gram 맞은 갯수)/(전체 corpus의 n-gram 갯수)가 된다.
BLEU는 0과 1 사이의 숫자를 내며, cadidate text가 reference와 얼마나 비슷한지 유사도를 말한다.
BLEU algorithm
BLEU는 여러개의 reference 번역과 candidate를 비교하여 정확도를 계산한다.
BLEU의 algorithm을 보기 전에 간단한 unigram precision을 구하고, 이 한계점을 고쳐나가면서 설명해보자
unigram precision
unigram precision은 다음처럼 정의된다.
- $m$: ref에서 찾은 candidate의 word의 갯수
- $w_t$: candidate에 있는 총 word 갯수
언뜻보기에는 이정도면 번역의 퀄리티를 평가하는데 괜찮지않나? 생각이 들지만 다음 반례를 보자.
문제점 1 - 번역은 안좋은데 unigram precision이 잘 나오는 경우
| Candidate | the | the | the | the | the | the | the |
|---|---|---|---|---|---|---|---|
| Reference 1 | the | cat | is | on | the | mat | |
| Reference 2 | there | is | a | cat | on | the | mat |
7개의 단어가 모두 두 reference에 나왔기 때문에 unigram precision은 다음과 같다.
BLUE는 여기서 몇가지 변경을 할 것이다.
clip_count
- $m_{max}$: 단어가 한 reference에서 나온 최대 갯수
- ex>
the의 경우 ref 1에 두번, ref 2에 한번 나와서 $m_{max}=2$이다.
- ex>
이를 사용해서 $m$을 clipping시킬 수 있다. 그러면
상당히 그럴싸해졌다!
문제점 2 - 짧은 번역문 선호
위처럼 고쳤을 때 짧은 번역문을 선호하는 문제가 또 있다. 예를들어, the cat이 나왔다고 하면,
이 된다.
bigram을 쓴다고 하더라고 $\frac{1}{1}$으로 여전히 1이다.
brevity penalty
그래서 length를 이용한 penalty를 준다. 다음 수식을 precision에 곱해줘서 페널티를 줄 수 있다.
- $r$: reference corpus의 length
- $c$: candidate corpus의 length
BLEU Implementation
이제 실제 구현으로 들어가보자.
- fetch_data
- geometric mean
- best_length_match
- clip_count
- ngram_precision
- brevity_penalty
- BLEU
fetch_data
data를 읽어온다.
import sys
import codecs
import os
import math
import json
def fetch_data(cand, ref):
""" Store each reference and candidate sentences as a list """
references = []
if os.path.isfile(ref):
with codecs.open(ref, 'r', 'utf-8') as reference_file:
references = reference_file.readlines()
else:
for root, dirs, files in os.walk(ref):
for f in files:
reference_file = codecs.open(os.path.join(root, f), 'r', 'utf-8')
references.append(reference_file.readlines())
candidate_file = codecs.open(cand, 'r', 'utf-8')
candidate = candidate_file.readlines()
return candidate, references
#testCode
cand, ref = fetch_data("golden.kr.pred.djamo", "golden.kr.bpe")
candidate = cand[0]
reference = ref[0]
print('cand: %r' %candidate)
print('ref: %r' %reference)
output:
cand: ‘범인이 현장에 무기를 두고 갔어\n’ ref: ‘공격자는 현장에 무기를 버렸다.\n’
geometric mean
기하 평균을 구한다. 이는 BLEU에서 1~4-gram에 대해 precision을 계산하는데, 이 4개의 기하 평균으로 최종 precision을 정하기 때문에 필요하다.
def geometric_mean(precisions):
return (reduce(operator.mul, precisions)) ** (1.0 / len(precisions))
geometric_mean([0.1, 0.2, 0.3, 0.4])
output:
0.22133638394006433
best_length_match
여러 개의 reference가 존재할 때, 가장 길이가 비슷한 reference를 찾는다. 이는 brevity penalty가 너무 크기에 필요한 것으로 보인다.
def best_length_match(ref_lens, cand_len):
'''
candidate랑 가장 길이가 비슷한 reference를 return
ref_lens: [3, 4, 5], cand_len : 4 => return 4
'''
least_diff = abs(cand_len-ref_lens[0])
best = ref_lens[0]
for ref_len in ref_lens:
if abs(cand_len-ref_len) < least_diff:
least_diff = abs(cand_l-ref_len)
best = ref_len
return best
clip_count
candidate의 n-gram마다 count를 세는데, 이 n-gram에 대한 reference의 max_count를 계산해서 clip한다.
마지막에 clip된 count들을 모두 더해주면 해당 sentence에 대한 count!
def clip_count(cand_d, ref_ds):
'''
arguments:
cand_d: {'나는': 1, '밥을': 1, '먹었다': 1}
ref_ds: [{'그는':1, '밥을':1, '먹었다':1},
{'그가': 1, '밥을':1, '먹었다':1}]
returns:
2 (나는 : 0, 밥을: 1, 먹었다: 1)
'''
count = 0
for key, value in cand_d.items():
key_max = 0
for ref in ref_ds:
if key in ref:
key_max = max(key_max, ref[key])
clipped_count = min(value, key_max)
count += clipped_count
return count
ngram_precision
위에서 본 clip_count를 사용해, 각 n-gram의 count를 구하고 이를 통해 precision을 구한다.
def ngram_precision(candidate, references, n):
'''
arguments:
candidate : ['cand1', 'cand2', ...]
references : [['ref1_1', 'ref2_1', ...],
['ref1_2', 'ref2_2', ...], ...]
n
returns:
precision for n-gram
'''
def _count_ngram(sentence, n):
'''
arguments:
sentence: 문장 string, ex> '나는 밥을 먹었다'
n: n-gram의 n. ex> 2
returns:
ngram_d: ngram의 dictionary. ex> {'나는 밥을': 1, '밥을 먹었다': 1}
'''
ngram_d = {}
words = sentence.strip().split() # '나는 밥을 먹었다' -> ['나는', '밥을', '먹었다']
leng = len(words) # 3
limits = leng - n + 1
for i in range(limits):
ngram = ' '.join(words[i:i+n]).lower() # n=2일 때, '나는 밥을', '밥을 먹었다'
if ngram in ngram_d.keys():
ngram_d[ngram] += 1
else:
ngram_d[ngram] = 1
return ngram_d
clipped_count = 0
count = 0
for si in range(len(candidate)): # si : sentence_index
ref_counts = [] # reference의 각 word별 count ex> [{'나는 밥을':1, '밥을 먹었다':1}]
for reference in references:
ngram_d = _count_ngram(reference[si], n)
ref_counts.append(ngram_d)
# candidate
cand_dict = _count_ngram(candidate[si], n)
n_ngrams = 0
for key, values in cand_dict.items():
n_ngrams += values
clipped_count += clip_count(cand_dict, ref_counts) # 각 n-gram당 max-count를 재고, clipping해서 더함.
count += n_ngrams # n-gram의 갯수
if clipped_count == 0:
pr = 0
else:
pr = float(clipped_count) / count
return pr
brevity penalty(BP)
length에 관한 penalty
- $r$: reference corpus의 length
- $c$: candidate corpus의 length
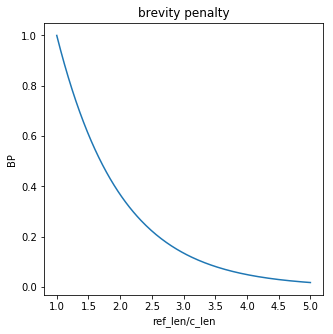
밑의 그림을 보면 알겠지만, reference의 length가 1.5배만 돼도 precision의 거의 40%를 페널티로 까먹는다.
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(1, 5, 200)
y = np.exp(1-x)
plt.figure(1, figsize=(5, 5))
plt.plot(x,y)
plt.title('brevity penalty')
plt.xlabel('ref_len/c_len')
plt.ylabel('BP')
plt.show()
import operator
from functools import reduce
def brevity_penalty(c, r):
if c > r:
bp = 1
else:
bp = math.exp(1-(float(r)/c))
return bp
def calculate_bp(candidate, references):
r, c = 0, 0
for si in range(len(candidate)):
ref_lengths = []
for reference in references:
ref_length = len(reference[si].strip().split())
ref_lengths.append(ref_length)
len_candidate = len(candidate[si].strip().split())
r += best_length_match(ref_lengths, len_candidate)
c += len_candidate
bp = brevity_penalty(c, r)
return bp
BLEU
- 1~4gram에 대해 precision을 구함.
- 위 4개의 결과에 대해 geometric mean을 구함
- brevity penalty를 구해서 precision에 곱해줌
def BLEU(candidate, references):
precisions = []
for i in range(4):
pr = ngram_precision(candidate, references, i+1)
precisions.append(pr)
bp = calculate_bp(candidate, references)
bleu = geometric_mean(precisions) * bp
return bleu, bp, precisions
candidate, references = fetch_data("golden.kr.pred.djamo", "golden.kr.bpe")
references = [references]
bleu, bp, pr = BLEU(candidate, references)
print("BLEU : {:.2f}, {}, (BP={:.3f})".format(bleu*100, ["{0:0.1f}".format(i*100) for i in pr], bp))
cands = []
for c in candidate:
cands.extend(c.split())
print("candidates의 word 갯수: {}".format(len(cands)))
refs = []
for r in references[0]:
refs.extend(r.split())
print("references의 word 갯수: {}".format(len(refs)))
print("word 갯수 비율: {:.3f}".format(len(cands)/len(refs)))
# BLEU = 7.08, 28.6/11.0/4.4/1.8 (BP=1.000, ratio=1.005, hyp_len=2127, ref_len=2117)
output:
BLEU : 7.08, [‘28.6’, ‘11.0’, ‘4.4’, ‘1.8’], (BP=1.000) candidates의 word 갯수: 2127 references의 word 갯수: 2117 word 갯수 비율: 1.005

 요렇게 만들면 Hidden까지의 Backpropagation은 똑같다.
요렇게 만들면 Hidden까지의 Backpropagation은 똑같다.