원문 torch.cuda는 현재 선택된 GPU를 계속 씁니다. 여기서 할당한 모든 CUDA tnesor들은 선택된 GPU안에서 만들어집니다. torch.cuda.device를 with절과 함께 사용하여 GPU 선택을 할 수 있습니다.

그러나 한번 tensor가 할당되면, 해당 tensor들을 사용한 operation들은 선택된 device와 관계없이 tensor들과 같은 device에 할당됩니다.

cross-GPU operation은 기본적으로 허용되지 않습니다. 그러나 copy_()를 쓰면 가능합니다. peer-to-peer memory access를 enable하지 않으면, 다른 device간에 퍼져있는 tensor들을 사용하는 operation은 error를 냅니다.

밑의 코드는 간단한 예제입니다.

x = torch.cuda.FloatTensor(1)
# x.get_device() == 0
y = torch.FloatTensor(1).cuda()
# y.get_device() == 0

with torch.cuda.device(1):
    # allocates a tensor on GPU 1
    a = torch.cuda.FloatTensor(1)

    # transfers a tensor from CPU to GPU 1
    b = torch.FloatTensor(1).cuda()
    # a.get_device() == b.get_device() == 1

    c = a + b
    # c.get_device() == 1

    z = x + y
    # z.get_device() == 0

    # even within a context, you can give a GPU id to the .cuda call
    d = torch.randn(2).cuda(2)
    # d.get_device() == 2

Best practices

pinned memory buffer를 사용하라

host에서 GPU로 카피하는 것은 pinned(page-locked) memory를 사용할때 훨씬 빠릅니다. CPU tensor들과 storage들은 pin_memory() method[pinned region에 data를 넣은 object의 카피를 리턴하는]를 노출합니다. (-그러나 실험 결과 그렇게 빨라지지 않음.)

또한, 한번 tensor와 storage를 pin하면, cuda()에 async=True로 하여 asynchronous GPU copy들을 쓸 수 있습니다. 이는 data transfer와 계산 겹치게 하기위해 쓰일 수 있습니다.(pipe-line을 얘기하는 것 같다.)

batch들을 생성하는 DataLoader를 pin_memory=True를 사용하여 생성하면, pinned memory에 위치시킬 수 있습니다.

Use nn.DataParallel instead of multiprocessing

batched input과 multiple GPU를 포함한 많은 케이스에 DataParallel을 기본으로 써보는게 좋습니다. GIL이 있더라도, 단일 python process가 multiple GPU를 충분히 돌릴 수 있습니다.

0.1.9 버전에서 8개 이상의 많은 GPU는 fully utilized가 아직 안되지만, 계속 개발중입니다.

multiprocessing 쓰지 마세요.

원문 Data parallelism은 mini-batch를 나누어 더 작은 여러개의 mini-batch로 나누고, 이들을 parallel하게 돌리는 것이다.

Data parallelism은 torch.nn.DataParallel에 구현되어있다. module을 DataParallel로 감싸면 알아서 잘 multi GPU로 parallelize해준다.

DataParallel

import torch.nn as nn

class DataParallelModel(nn.Module):

    def __init__(self):
        super().__init__()
        self.block1 = nn.Linear(10, 20)

        # block2만 DataParallel을 한다.
        self.block2 = nn.Linear(20, 20)
        self.block2 = nn.DataParallel(self.block2)

        self.block3 = nn.Linear(20, 20)

    def forward(self, x):
        x = self.block1(x)
        x = self.block2(x)
        x = self.block3(x)
        return x

이 코드는 CPU-mode로 바꿀 필요가 없다.(?)

보통, pytorch의 nn.parallel primitive는 각자 쓸 수 있다. 우리는 simple MPI-like primitive들을 구현했다.

• replicate : 모듈을 여러 디바이스에 복사
• scatter : input을 첫번째 dimension으로 나누어 분산
• gather : input을 모아서 첫번째 dimension 기준으로 concatenate
• parallel_apply : 이미 분산된 input을 이미 분산된 모델에 적용

더 확실하게 하기위해, data_parallel 함수를 위의 primitive들로 구성한 것이다.

찾아보니 실제로 거의 비슷하게 구현되어있음.

def data_parallel(module, input, device_ids, output_device=None):
    if not device_ids:
        return module(input)

    if output_device is None:
        output_device = device_ids[0]

    replicas = nn.parallel.replicate(module, device_ids)
    inputs = nn.parallel.scatter(input, device_ids)
    replicas = replicas[:len(inputs)]
    outputs = nn.parallel.parallel_apply(replicas, inputs)
    return nn.parallel.gather(outputs, output_device)

CPU와 GPU를 모두 쓰는 model

이제 cpu/gpu를 모두 쓰는 예제를 살펴보자.

class DistributedModel(nn.Module):

    def __init__(self):
        super().__init__(
            embedding=nn.Embedding(1000, 10),
            rnn=nn.Linear(10, 10).cuda(0),
        )

    def forward(self, x):
        # Compute embedding on CPU
        x = self.embedding(x)

        # Transfer to GPU
        x = x.cuda(0)

        # Compute RNN on GPU
        x = self.rnn(x)
        return x

원문

Attention Mechanism

2015년 딥러닝과 AI의 진보에 따라, 많은 연구자들이 뉴럴넷의 <<attention mechanism>>에 관심을 가지고있다. 이 포스트는 어텐션 메카니즘이 무엇인지 high-level의 설명을 주는 것이 목표이며, 또한 attention의 계산에 관한 기술적인 몇가지 스텝들을 소개할 것이다.

만약 더 많은 수식과 예제를 원한다면 reference가 더 많은 디테일한 정보를 줄 것이다. [3] 불행하게도, 이러한 모델들은 항상 구현이 쉽지는 않고 몇개의 오픈소스로 된 구현들이 릴리즈되어있다.

Attention

attention을 포함한 neural process들은 신경과학과 Computational Neuroscience(뇌의 기능을 연구한다는데 적절한 단어를 모르겠네요..) 분야에서 연구되고 있었다. 특정 연구분야는 visual attention가 있다: 많은 동물들이 적절한 반응을 계산하기 위해 영상 신호에 대해 일부분만 집중한다. 이 원칙은 neural computation에서 큰 영향을 가져왔다.[정보를 모두 쓰기보다는 일부분만 가져와야했기 때문에] 입력값의 특정 부분에 집중하는 비슷한 아이디어가 딥러닝에 도 적용이 되어있다.[음성 인식, 번역, 추론(?), 물체 인식]

Attention for Image Captioning

이제 attention mechanism의 예제를 보자. 우리가 하고픈 일은 image captioning이다.

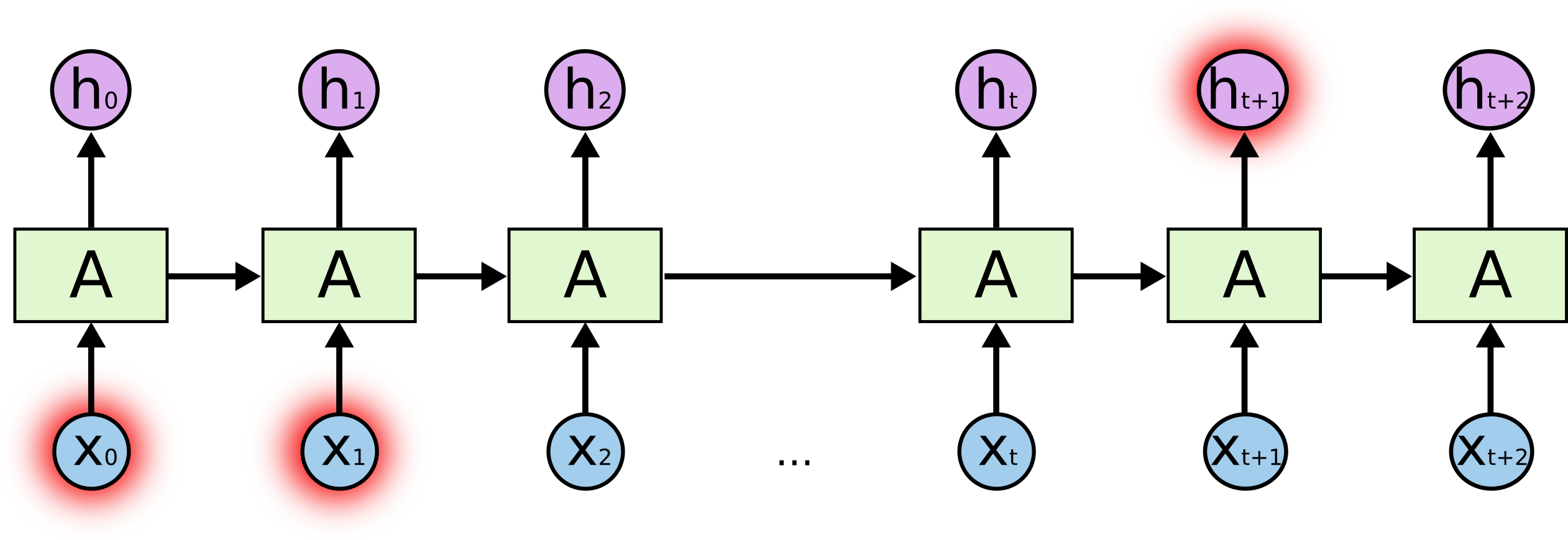
예전 image captioning system은 미리 학습한 CNN[hidden state h를 내는]을 이용해 image를 encode했다. 그리고는 그 state를 RNN을 써서 decode한다. 재귀적으로 caption을 생성한다. 이런 method는 [11]을 포함한 몇몇 그룹들이 사용했다. (아래 그림을 보라)

문제는 [모델이 자막의 다음 단어를 생성할 때, 이 단어는 보통 이미지의 일부분만을 묘사한다는] 것이다. (의역) 이미지의 전체 representation h를 사용하면 각 단어들을 효과적으로 생성할 수 없다. 이럴 때 attention mechanism이 도움이 된다.

attention mechanism을 사용하면, 이미지는 n개의 부분으로 나뉘어지고, CNN[각 파트에 대한 표현 $h_1,…,h_n$을 생성하는]을 거친다. RNN이 새로운 단어를 생성할 때, attention mechanism이 이미지의 연관된 부분에 집중하고, decoder는 이미지의 특정 부분만을 사용한다.

아래 이미지의 윗쪽 열에서, 각 단어에 대해 어떤 이미지(하얀색)가 사용되었는지 알 수 있다.

다른 예제로, 이미지의 어떤 부분이 밑줄친 단어를 생성하는데 쓰였는지 볼 수 있다.

이제 attention model이 어떻게 동작하는지 설명할 차례이다[일반적인 설정에서]. 복잡한건 [3]을 가보라.

attention model이 뭐에요?

어텐션 모델은 무엇일까? 어텐션 모델은 방법[n개의 인자 $y_1,…,y_n$와 context $c$를 받아서 vector $z$를 내는]이다. 이 때, $z$는 $y_i$의 summary[c와 연관된 정보를 집중하는]로 생각된다. 더 formmal하게, 어텐션 모델은 yi의 weighted arithmetic mean을 반환하며, weight는 주어진 context c에 대한 각 $y_i$의 연관도에 따라 설정된다.

앞서 설명한 예제에서, context는 생성된 문장의 처음을 말하여, $y_i$는 각 이미지 부분들의 표현($h_i$)이고, output은 filtered image의 표현이다. 이 때, filter는 생성된 단어가 관심있는 부분을 포커싱한 것을 말한다.

attention model의 한가지 흥미로운 특징은 산술평균의 weight가 접근가능하며 plot이 가능하다는 것이다. 이는 앞서 본 이미지에서 하얀 색으로 색칠된 부분과 일치한다.

그래서 이 블랙박스가 정확히 어떻게 동작하나? attention model의 전체 그림은 다음과 같다.

네트워크가 복잡해보이는데 차근차근 설명할테니 걱정마시라.

먼저 입력부터 살펴보자. c는 context, y_i는 데이터의 일부분이다.

다음 스텝으로, 네트워크는 $m_1, …, m_n$을 계산[tanh 레이어를 통해]하는데 이는 c와 y_i의 값의 집단을 계산하는 것을 의미한다. 여기서 $m_i$를 계산할 때, $y_i$만 보고 다른 $y$는 보지 않는다.

이제 softmax를 계산한다. softmax는 argmax와 비슷한 양상을 보이지만, 미분이 가능하다. (softmax 설명 생략)

이제 $s_i$와 $y_i$를 곱해서 모두 더하면 output z가 나오게 된다.

relevance의 다른 계산법

위에 설명한 attention model은 변경 가능하다. 먼저 tanh를 바꿔볼 수 있다. 딱 한가지 중요한 것은 c와 y_i를 믹싱하는 함수라는 것이다. 여기서 사용한 것은 c와 y_i의 dot product이다.

이 모델이 더 이해하기 쉬운데, context와 가장 관련 깊은 변수를 softly-choosing한다는 것이다. 다른 중요한 버전은 hard attention이다.

soft attention & hard attention

위에 보여준 메카니즘을 soft attention이라 부른다. 왜냐면 전부 미분가능하며, attention mechanism을 통해 gradient가 흘러갈 수 있기 때문이다.(의역)

hard attention은 stochastic process이다: 모든 hidden state들을 decoding의 input으로 쓰는 대신에, hidden state $y_i$를 확률 $s_i$로 샘플링해서 쓴다. gradient를 구하기 위해서는 몬테카를로 sampling으로 gradient를 추정해야한다.

두 시스템 모드 장단점이 있는데, 현재는 gradient를 직접적으로 계산할 수 있는 soft attention을 더 많이쓴다.

image captioning으로 돌아가보자!

이제 앞서 보인 image captioning system이 어떻게 동작하는지 이해가 가능할 것이다.

(그림에 대한 설명 생략)

기계 번역에서의 align

Bahdanau[5]가 제안한 neural translation model도 attention을 쓰고있다.

먼저 attention을 쓰지 않은 신경망 번역을 보자. encoder[RNN을 쓰는]는 영어 문장을 입력으로 받아서 hidden state h를 제공한다. 이 hidden state h는 decoder RNN이 옳은 output 프랑스 문장을 만들도록 조정한다.

번역에서, image captioning과 같은 생각을 할 수 있다. 새로운 단어를 만들 때, 우리는 보통 원문에 있는 하나의 단어를 번역한다. attention model은 새로운 단어를 만들 때, 원문의 일부분에 집중하도록 만들어준다.

전체 문장에 대한 단 하나의 hidden state를 제공하는 대신, incoder는 각 단어에 해당하는 hidden state $h_j$를 제공한다. decoder RNN이 단어를 생성할 때마다, 각 hidden state의 공헌도를 결정하고, 보통 그것은 하나의 state를 뽑는다.(밑의 그림을 보라) softmax를 사용한 공헌도는 attention weight $a_j$를 의미하며, hidden state $h_j$는 decoding에 weight $a_j$만큼 기여한다.

이 케이스에서, attention mecanism은 전부 미분가능하며, 다른 supervision을 필요치않는다. 그저 Encoder-decoder 모델의 위에 추가된 것이다.

이 방식은 alignment라고도 볼 수 있는데, 네트워크가 새 단어를 만들어내는 매 스텝마다 보통 하나의 input 단어에 집중하기 때문이다. 이것은 거의 대부분의 weight가 0이며, 하나의 weight만 활성화됨을 의미한다. 밑의 그림은 번역 중의 attention weight를 보여준다.

RNN이 없는 attention

여태까지 encoder-decoder에 들어간 attention model만 설명했다. 그러나, input의 순서는 중요하지 않으려, 독립된 hidden states $h_j$에 대해서도 가능하다. (의역)Raffel[10]의 경우가 그러한데 attention model이 fully feed-forward이며, memory-network의 간단한 예시에서도 드러난다.

from attention to memory addressing

이 부분은 생략…

##Final word

attention mechanism과 fully differentiable addressable memory system은 현재 많은 연구자들이 연구중이다. 아직 나온지 얼마 안되고, 구현이 덜 되었음에도, 이것이 많은 문제들의 state of the art를 달성하는 것을 보여주었다.

이후도 생략…

원문

RNN의 Long-term dependencies 문제

RNN의 식을 간단히 살펴보자

hidden state를 거치는데, $h_{t}$와 $x_{t}$에 $\tanh$를 한 녀석이 들어가기 때문에, 한참 뒤의 output에 반영이 되기에 어렵다. 물론 이론상으로는 long-term dependency를 잘 핸들하도록 파라미터 튜닝을 잘 하면 된다고 하지만 그래도 어렵다.

LSTM Networks

이를 해결하기 위해 LSTM이라는 RNN의 변형이 나오게 된다. 기존의 RNN과 비교를 해보자.

간단히 그림으로만 봐도, 윗쪽 라인은 non-linear한 연산이 없이 쭉 유지된다. 그렇기에 long term을 잘 유지할 수 있어보인다.

윗쪽 라인은 Cell state, 아랫쪽 라인은 output state이다.

Cell state

1번째 세로줄

처음 라인을 보면 Sigmoid연산을 하는데, 이는 0~1 사이의 값을 준다. 거기에 곱셈 연산이니까, 어느정도의 양을 계속 가져갈 것인지 정하는 구간이다. $f_t = \sigma ( W_f \cdot [h_{t-1}, x_t] + b_f)$

2,3번째 세로줄

여기서는 어떤 새로운 정보를 저장할 것인지 정한다.

input gate layer($i_t$) : 값을 update할 것인지 정한다. $i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$ tanh layer($\tilde{C_t}$) : 새로운 후보 값을 만든다. $\tilde{C_t} = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)$

최종

위의 두개를 합쳐서 Cell state가 업데이트된다. $C_t = f_t * C_{t-1} + i_t * \tilde{C_t}$

output state

이제 이를 내보낸다. 식만 써놓자..

01. softmax classifier와 neural network 구현

02. SVM 구현

원문

NN의 다양한 구현체들 예제

1. RNN 없는 그냥 NN. 고정된 input, output size를 가진다.
2. Sequence output (예> image captioning: input은 image 한장이고 output은 word들이 있는 문장)
3. Sequence input (예> sentiment analysis: sentence를 input으로 하고 positive인지, negative인지 구분짓는 것)
4. Sequence I/O (예> machine translation : RNN이 영어 문장을 읽고, 프랑스어로 output 문장을 낸다.)
5. Synced sequence I/O (예> video classification: 각 프레임에 label을 붙이고 싶음)

RNN Computation

RNN은 그저 input x를 받아서 output y를 return하는 함수이다. 그런데 y를 내는데에 있어서 현재 넣은 input뿐만이 아니라, 과거의 input또한 영향을 미친다. RNN class를 만든다면, step이라는 함수는 x를 받아 y를 낸다.

rnn = RNN()
y = rnn.step(x) # x is an input vector, y is the RNN's output vector

RNN은 매 step마다 업데이트되는 internal state를 가진다. 가장 단순한 것으론 vector h하나를 state로 갖는다. 다음 것은 RNN의 가장 단순한 구현이다.

class RNN:
    # ...
    def step(self, x):
        # update the hidden state
        self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
        # compute the output vector
        y = np.dot(self.W_hy, self.h)
        return y

위는 vanila RNN의 forward pass를 구현한 것이다. self.h는 0으로 초기화하며 나머지 matrix는 random하게 초기화한다. RNN에서 hidden state를 구하는 식은 다음과 같다. $h_t = \tanh ( W_{hh} h_{t-1} + W_{xh} x_t )$ 이후 hidden state로 output을 구하는데 식은 다음과 같다. $y_t = W_{hy} \cdot h_t$

Going Deep

더 딥하게 쌓으려면 단순히 다음처럼 하면 된다.

y1 = rnn1.step(x)
y = rnn2.step(y1)

이제 코드를 짜보자!

loss와 다음 state에 대한 gradient를 가지고있다는 것을 생각해보자.

def lossFun(inputs, targets, hprev):
    xs, hs, ys, ps = {}, {}, {}, {}
    hs[-1] = np.copy(hprev)
    loss = 0
    # forward pass
    for t in xrange(len(inputs)):
        xs[t] = np.zeros((vocab_size,1)) # encode in 1-of-k representation
        xs[t][inputs[t]] = 1
        hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1]) + bh) # hidden state
        ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
        ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
        loss += -np.log(ps[t][targets[t],0]) # softmax (cross-entropy loss)
    # backward pass: compute gradients going backwards
    dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
    dbh, dby = np.zeros_like(bh), np.zeros_like(by)
    dhnext = np.zeros_like(hs[0])
    # gradient는 역으로 계산한다. (당연히 backpropagation이니까)
    for t in reversed(xrange(len(inputs))):
        # dscore for loss
        dy = np.copy(ps[t])
        dy[targets[t]] -= 1
        # 나머지...
        dWhy += np.dot(dy, hs[t].T)
        dby += dy
        #loss말고 전의 state에서 발생한 gradient를 더해준다.
        dh = np.dot(Why.T, dy) + dhnext # backprop into h
        # 또 나머지...
        dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity (tanh' = 1-tanh^2)
        dbh += dhraw
        dWxh += np.dot(dhraw, xs[t].T)
        dWhh += np.dot(dhraw, hs[t-1].T)
        dhnext = np.dot(Whh.T, dhraw)  # hs[t-1]에 대한 미분값

    for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
        np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
    return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs)-1]