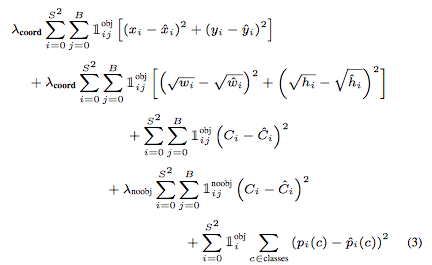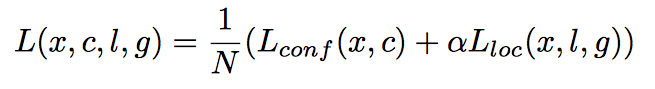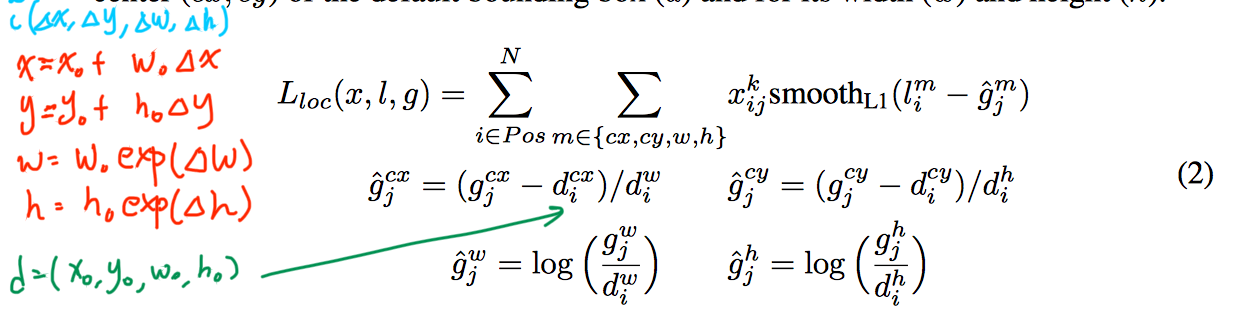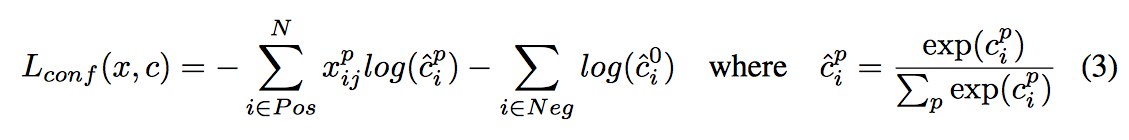09 Mar 2018
|
python
list
python list를 어떻게 효율적으로 쓸까 고민하다가 list에 대해서 공부를 좀 했다.
궁금증은 다음 두 가지였다.
- python list의 구조는 어떻게 생겼는지… item 갯수를 알 때 효율적으로 넣는 방법(preallocation)
- python list의 처음 alloc size와 append의 동작 방식
python list 구조와 preallocation
사실 처음에 preallocation을 하려면 어떻게 할까 찾아봤는데, 답변들이 [None] * size를 쓰면 된다고 했다. 이러면 size가 다른 객체들을 어떻게 넣지? 의문이 생겼고, 그래서 생긴 꼴을 찾아봤다.
참조 1 - PyListObject 구조를 보면 다음처럼 생겼다.
typedef struct {
PyObject_VAR_HEAD
PyObject **ob_item;
Py_ssize_t allocated;
} PyListObject;
대충 봐도 pointer로 item들을 가지고 있겠거니… 생각이 들며 다음 코드를 보면 확실해진다.
참조 2 - python list setitem
PyList_SetItem(PyObject *op, Py_ssize_t i,
PyObject *newitem)
{
PyObject **p;
if (!PyList_Check(op)) {
Py_XDECREF(newitem);
PyErr_BadInternalCall();
return -1;
}
if (i < 0 || i >= Py_SIZE(op)) {
Py_XDECREF(newitem);
PyErr_SetString(PyExc_IndexError,
"list assignment index out of range");
return -1;
}
p = ((PyListObject *)op) -> ob_item + i
Py_XSETREF(*p, newitem);
return 0;
}
마지막 세 줄을 보면
- pointer를 옮기고
- item을 포인팅하고
- return
이다.
따라서 [None] * size는 포인터 배열을 한번에 alloc하는 정도로, append 시 포인터 배열 realloc에 대한 overhead만 줄여준다.
python list의 처음 alloc size와 append의 동작 방식
그러고보면 처음에 얼마나 메모리를 잡고있으며, append를 하면 어떻게 메모리를 할당하나 궁금해졌다.
결론은
- 처음에는 한칸도 alloc하지 않는다.
- 하나라도 append를 하면 4개를 alloc한다.
- 그 뒤로 4개 이상 들어오면 8개로 realloc하며, 이를 반복!
요런 식으로 동작한다.
알아본 방법은 코드로 대체한다.
Python 3.5.3 (default, Jan 17 2018, 16:36:00)
[GCC 5.4.0 20160609] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import sys
>>> l = [None] * 10
>>> l
[None, None, None, None, None, None, None, None, None, None]
>>> sys.getsizeof(l)
144
>>> sys.getsizeof(None)
16
>>> a = []
>>> sys.getsizeof(a)
64
>>> b = [None] * 100
>>> sys.getsizeof(b)
864
>>> a = [1]
>>> sys.getsizeof(a)
72
>>> a = []
>>> a.append(1)
>>> sys.getsizeof(a)
96
12 Feb 2018
|
python
repr
dict
Obeject의 속성값을 알고싶은데…
Obeject의 속성값을 알고싶은데 print()로 찍어보면 <__main__.OrigClass object at 0x10bedd0b8>이런 식으로만 나온다.
이럴 경우, __repr__을 통해 알 수 있도록 만들 수 있다.
물론 __repr__은 eval함수에 넘겼을 때, 정확히 똑같은 object가 만들어지는 string representation을 만들도록 권장한다. __dict__함수를 사용해서 속성을 볼 수도 있다!
코드
class OrigClass(object):
def __init__(self, x=0, y=0):
self.x = x
self.y = y
class RepresentativeClass(OrigClass):
def __repr__(self):
return "RepresentativeClass({}, {})".format(self.x, self.y)
if __name__ == '__main__':
o = OrigClass(10, 20)
r = RepresentativeClass(10, 20)
print(o) # 그냥 돌리니까 메모리 주소만 나오겠지...
print(r) # 요 경우 RepresentativeClass(10, 20)가 나오겠다..
r2 = eval(repr(r)) # 이걸 다시 eval에 넘기면
print(r2) # 같은 attr을 갖는 객체를 만들 수 있다!
print(o.__dict__) # 속성값만 알고싶을 때..
결과값
<__main__.OrigClass object at 0x106f1e0b8>
RepresentativeClass(10, 20)
RepresentativeClass(10, 20)
{'y': 20, 'x': 10}
05 Feb 2018
|
ml
segmentation
rcnn
ssd
yolo
History
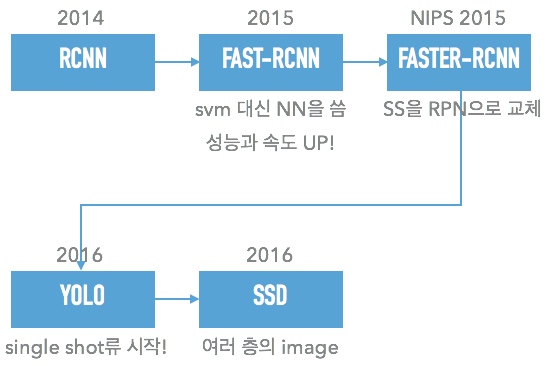
R-CNN류
R-CNN
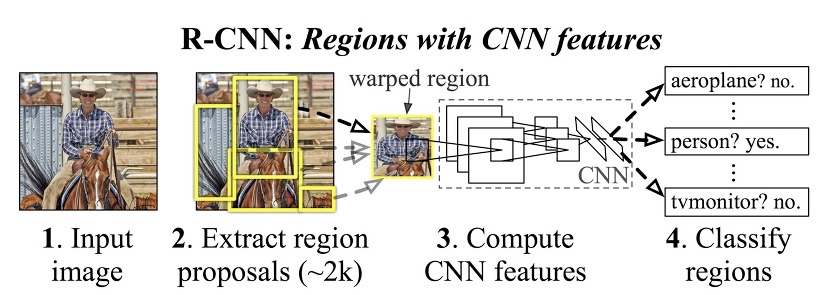
- CNN fine-tuning (3번에 쓰일 Classifier)
- Selective search로 ROI 계산
- ROI들을 warp해서 (2)CNN에 넣고 feature extract를 수행한다.
- 분석된 Feature들을 softmax classifier나 SVM에 붙여서 각 proposal의 score를 매긴다.
- Non-Maximum Suppression(NMS)을 이용하여 bounding box를 구한다.
NMS 예제 
- 문제점
- CNN, SVM, BB regressor등을 훈련해야함.
- 비슷한 박스들을 CNN돌리니까 느려…
Fast R-CNN
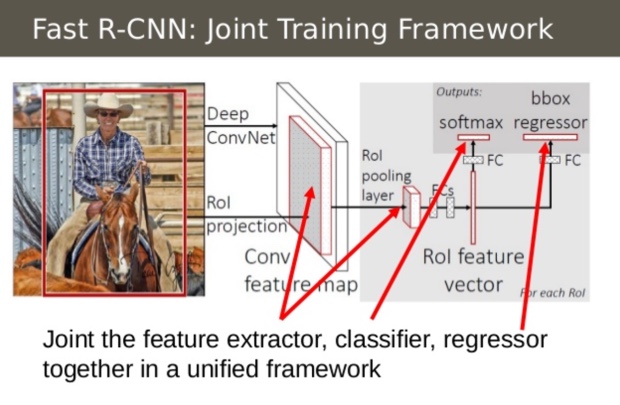
- CNN network를 전체 이미지에 대해서 한번에 하고 ROI를 즐 뽑아내면 CNN 돌리는 시간이 줄어듬
- SVM, BBR을 하나의 network로 트레이닝함
Faster R-CNN
Selective Search가 Bottleneck이다. 이를 뒤에있는 CNN의 weight를 이용해서 구현하면 훨씬 빠르고 쉬워진다! -> Region proposal network(RPN)
단점
Selective search를 하든, RPN을 쓰든 어쨌든 느리다. 그래서 사실 논문을 제대로 안보고 스킵스킵…
Single Shot Detector류
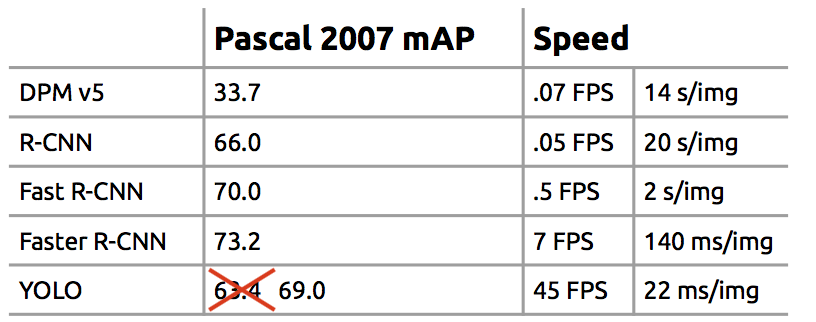 Single Shot Detection으로 오면서 7fps가 45fps로 껑충 뛰게된다.참조 슬라이드
Single Shot Detection으로 오면서 7fps가 45fps로 껑충 뛰게된다.참조 슬라이드
YOLO (You only look once)
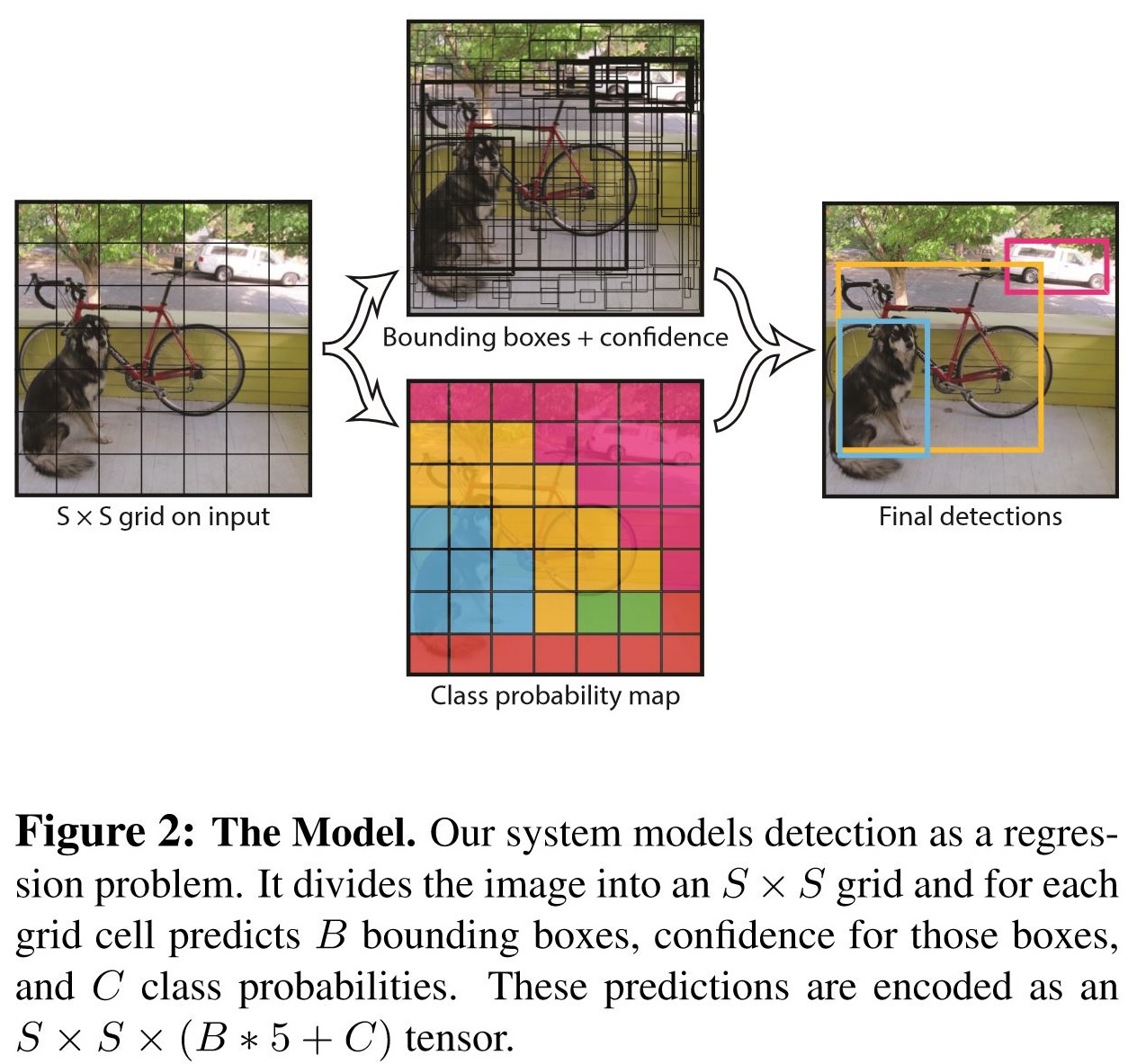
- 이미지를 grid로 나눠서, 해당 grid안에 center가 있는 boundingbox들의 위치와 confidence를 학습시킴
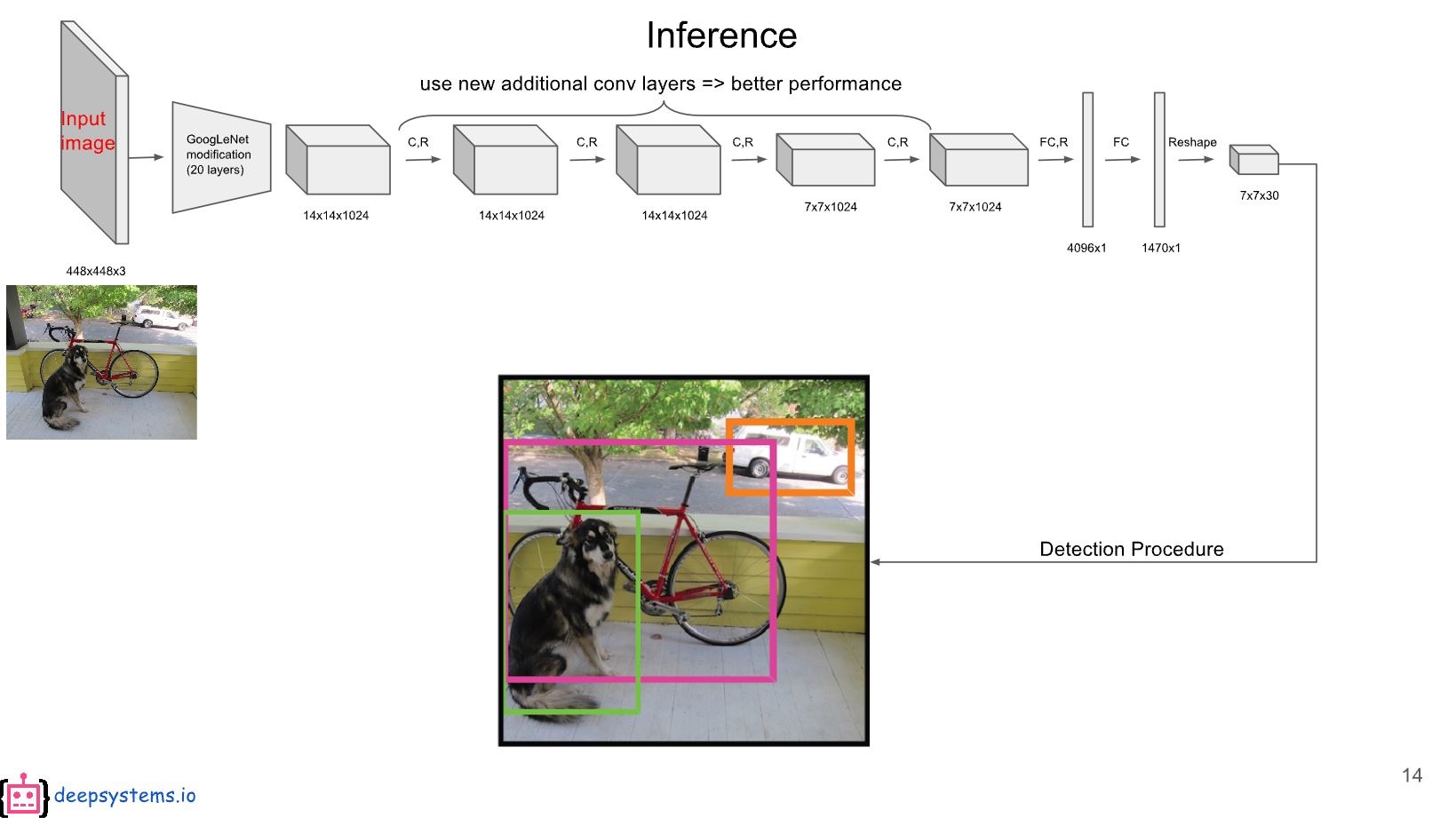
- 처음에는 VGG를 가져다쓰고, 이를 CNN Layer 여러개를 거치고, FC를 하면 7x7x30의 feature가 나온다.
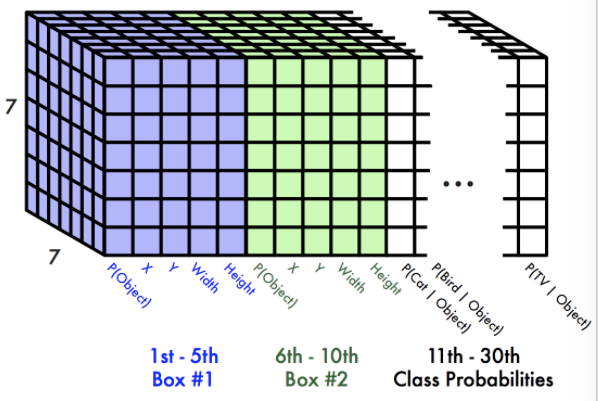
- 여기서 하나의 그리드에 30이 나오는데
- [2개의 bounding box(각각 5개 x,y,w,h,c) + 20개의 class에 대한 conditional class prob.]를 의미한다.
-
c는 해당 BB의 confidence 즉,p(object). 설명 안하고 넘어갔는데, 사실 bounding box의 확률은, object가 존재하는지와, 해당 object가 어떤 class인지 두가지로 나뉘어져있다.
- 요걸 가지고 비슷한 box에 대해서 Non-maximum suppression을 하면 완성!
loss
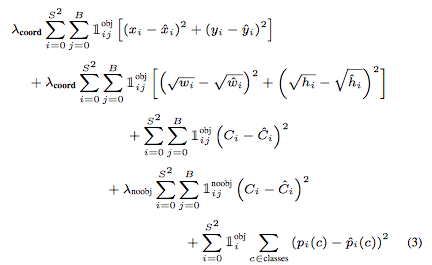
- object가 존재할 때, center 차이의 제곱
- object가 존재할 때, width, height의 root의 차이의 제곱
- object가 존재할 때, Confidence score 계산(Ci가 1)
- object가 존재하지 않을 때, Confidence score 계산(Ci가 0)
- object가 존재할 때, 각 class의 확률 차이의 제곱
Limitation of YOLO
베껴옴
- 각각의 grid cell이 하나의 클래스만을 예측할 수 있으므로, 작은 object 여러개가 다닥다닥 붙으면 제대로 예측하지 못한다.
- bounding box의 형태가 training data를 통해서만 학습되므로, 새로운/독특한 형태의 bouding box의 경우 정확히 예측하지 못한다.
- 몇 단계의 layer를 거쳐서 나온 feature map을 대상으로 bouding box를 예측하므로 localization이 다소 부정확해지는 경우가 있다.
SSD(Single Shot multibox Detector)
- Yolo와 거의 비슷하나, Convolution layer의 중간중간에서 모두 feature를 뽑는 점이 크게 다르다.
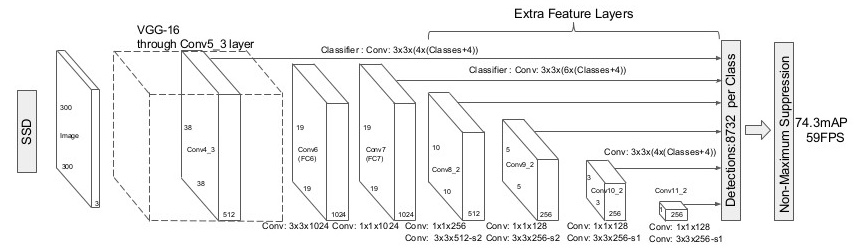
- 위의 그림에서 Detections에 들어가는 화살표가 convolution layer 사이사이에 존재함.
- 또한 각 grid에서는 location관련정보 4개[∆(cx, cy, w, h)]와 각 class의 confidence로 이루어진다.
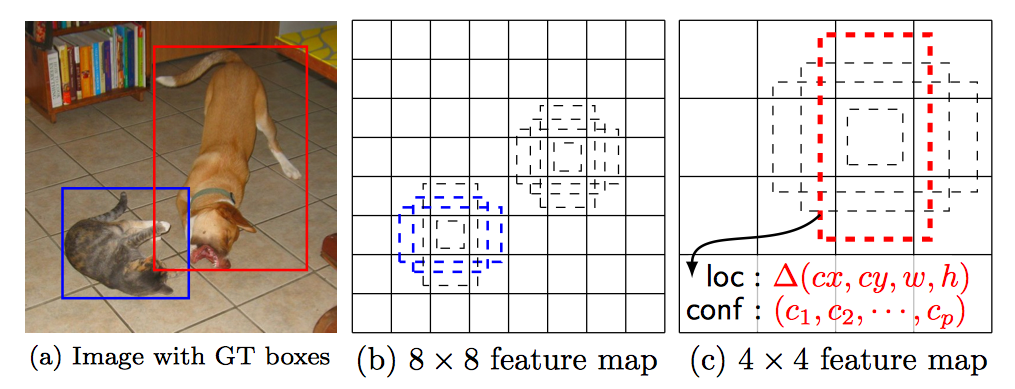
- 좀 더 자세히 알고싶으면 여기…
loss 계산
- confidence와 location error를 loss로 씀
- location error
- confidence error
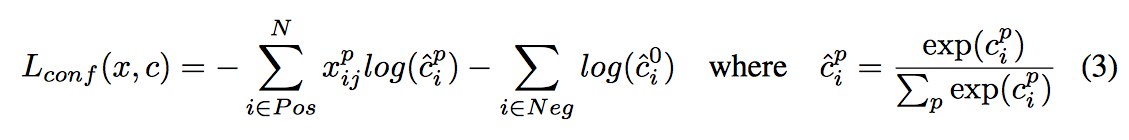
smooth-L1 loss는 0 근처에서 quadratic인 l1 loss의 변형이다.







 Single Shot Detection으로 오면서 7fps가 45fps로 껑충 뛰게된다.
Single Shot Detection으로 오면서 7fps가 45fps로 껑충 뛰게된다.