30 Jan 2018
|
ml
rnn
배경 설명
- RNN은 sequence learning을 잘 할 수 있음
- 근데 segmentation이 안되어있으면, 학습이 힘들다.
- 그래서 segmentation을 하려고 하니 데이터를 많이 만들기 힘들다.
- 아래 그림처럼 unsegmented data를 바로 학습할 수는 없을까?
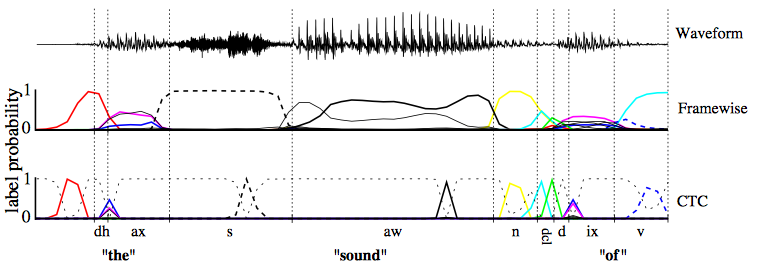
접근방법
- input도 variable, output도 variable인데, 가능한 align을 모두 뽑아서 marginalize하면 됨!
2. Temporal Classification
Temporal domain에 있는 것들을 classify하기 위한 정의 (Kadous, 2002)
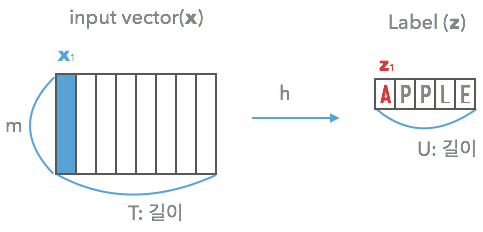
- input space $\cal{X} = (\mathbb{R}^m)^*$
- $\cal{Z} = L^*$
- $S$
- 고정된 distribution $D_{\cal{X} \times \cal{Z}}$에서 뽑힌 학습셋
라고 하면 $S$는 $(\textbf{x}, \textbf{z})$들로 이루어져있지.
- $\textbf{z} = (z_1, … , z_U)$
- $\textbf{x} = (x_1, … , x_T)$
$U \le T$ 여야함. 나중에 CTC_LOSS 정의를 보면 알겠지만..
목표
$S$를 사용하여 $h: \cal{X} \rightarrow \cal{Z}$를 학습시킴
2.1. Label Error Rate(LER)
- $S’ \subset D_{\cal{X} \times \cal{Z}}$를 S와는 다른 test set이라 하고,
- $Z$는 $S’$의 전체 갯수라 하면
여기서 $ED$는 Edit distance이다.
3. Connectionist Temporal Classification
RNN과 blank를 이용
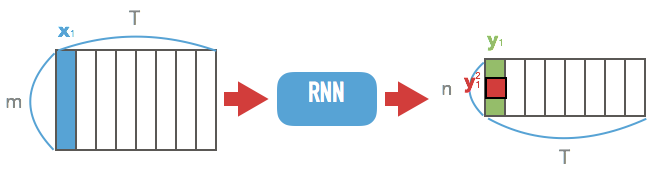
- $\cal{N}_w$: m차원 vector를 n차원으로 줄이는 RNN
- $\textbf{x}$를 넣으면
- $n\times T$의 matrix가 나옴.
- 이제 $\textbf{y} = \cal{N}_w(\textbf{x})$라 하면
- $y_k^t$: t번째 step의 k번째 label의 probability
-
-
$L’$는 $L$에서 blank가 추가된 것!
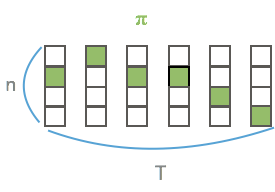
many-to-one map $\cal{B}$
- $\cal{B}$: $L’^T \rightarrow L^{\le T}$
- $L^{\le T}$: 가능한 labeling의 집합.
- 방식: blank와 반복되는 label을 제거
- $\cal{B}(a−ab−) = \cal{B}(−aa−−abb) = aab$
- 요렇게 되면 당연히 many-to-one의 관계!
이제 위의 $\cal{B}$를 통해 $\textbf{l} \in L^{\le T}$의 probability를 구할 수 있다!!!!
-
- label $\textbf{l}$에 해당하는 모든 $\pi$에 대해서 summation을 하면 된다.
3.2. Constructing the Classifier
여기까지 했으면 $h$는 단순히 다음처럼 끝난다.
$\textbf{l}$을 가능하게 하는 모든 path들의 확률을 더해서 이 중 argmax를 찾음.
- 아쉽게도, 이 수식에는 many-to-one인 $\cal{B}$의 역함수를 쓰게되며, 계산이 어려워진다.
- 따라서 approximation을 쓰게되는데, 다음 두가지가 존재한다.
- $h(\textbf{x}) \sim \cal{B}(\pi^*)$
- where
- 수식으로 보니까 헷갈리지만 단순히 RNN에서 max probability를 뽑고, 그것을 $\cal{B}$에 태운 것!
- prefix search decoding
- 4.1에서 설명할 forward-backward algorithm을 수정한 것
- 계산시간이 느림…
- 좋은 방법 없나?
- dynamic programming으로 해결한다.
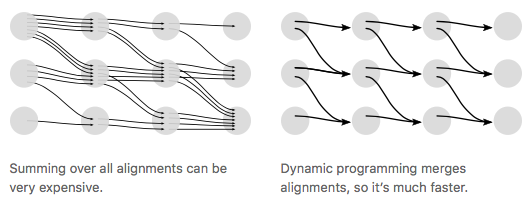
- 사진 출처
4. Training the Network
4.1. The CTC Forward-Backward Algorithm
$p(\textbf{l}\ \vert\ \textbf{x})$를 구하는 효율적인 알고리즘!
forward variable $\alpha_t(s)$
엄청 헷갈려 보이나 잘 뜯어보면
- Summation 아래:
- $N^T$: $\pi$의 1~t까지가 label의 1~s를 만족하는 path의 set
- 그 안의 $\pi$에 대해서 summation
- Pi는:
결국 $\alpha_t(s)$란 1:t까지 가면서 label $\textbf{l}_{1:s}$를 만들 확률을 의미한다.
이제 label의 각 사이사이와 앞, 뒤에 blank를 붙여서 $\textbf{l}’$를 만들고 이 녀석에 대해서 forward 계산을 할 것이다.
나중에 보면, 이렇게 해야 여러 path가 나온다.
그러면
- $\alpha_1(1) = y_b^1$
- $\alpha_1(2) = y_{\textbf{l}_1}^1$
- $\alpha_1(s) = 0\ \ \ \ \ \forall s > 2$
이며 자연스럽게 아래 triangle은 0가 된다.
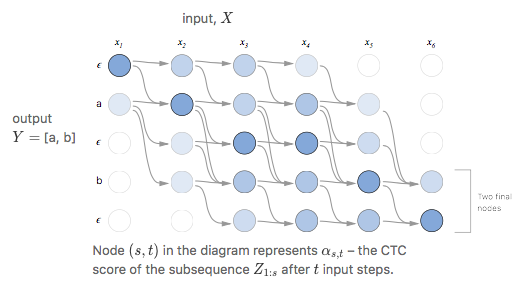 사진 출처
사진 출처
그리고 recursion을 할 수식은 다음과 같다.
-
-
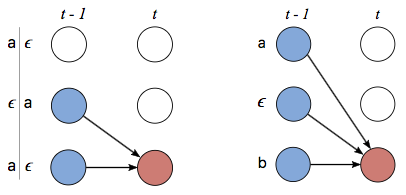 사진 출처
사진 출처
- 여태까지 설명한 것은 forward를 구하는 방법인데, 이는 사실 network output의 1:t가 label의 1:s일 확률을 구했다고볼 수 있다.
- $t:T$가 label의 $s:\vert l\vert$일 확률을 구하는 것이 backward인데, 이는 forward와 수식전개가 거의 똑같으므로 딱히 설명하지 않겠다.
- $\beta_t(s)$로 표기한다는 것만 알아두자.
또 underflow를 방지하기위해 각자 normalize해서 쓴다고한다. 별 중요한 얘기는 아님
4.1. Maximum Likelihood Training
forward-backward variable로 $p(\textbf{l} \vert \textbf{x})$ 표현하기
- 이제 forward-backward를 곱하고 $y_{\textbf{l’}_s}^t$로 나누면 (s자리는 겹치니까.. 당연히 나눠줘야지)
-
- 번역해보면 t번째 output이 label의 s번째일 때, label이 나올 확률
- 그러면
-
- 그래서 미분하면…
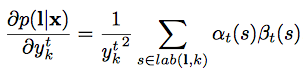
MLE 계산
- 이제 실제로 gradient를 구해보자
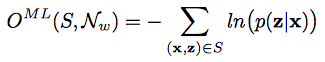
- 요걸 $(x,z) \in S$에 대해서 미분하면..
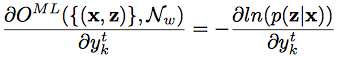
- 위의 식을 요걸로 치환하고, $\textbf{l} = \textbf{z}$니까..
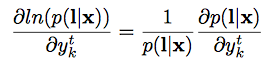
- 요렇게 된다고 한다.(귀찮아서 안따라가봄… $u_k^t$는 $y_k^t$의 unnormalized probability.
오타가 아니다)
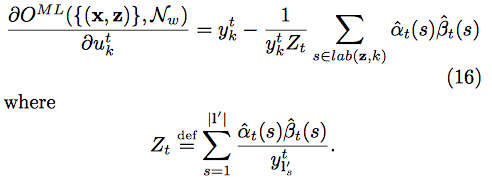
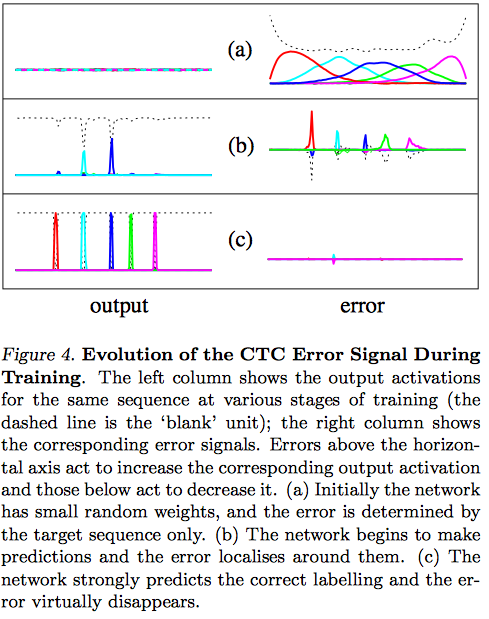
- 여기서 (16)은 error signal로, 학습중에 유용하게 쓰인다고 함
21 Jan 2018
|
makefile
가장 기본
<target>: <prerequisite>
<recipe> # 앞에 무조건 탭!!
- target
- 작업의 제목
- 보통 새로 만들어질 output filename으로 한다.
- prerequisite
- recipe
vi에서 tab을 강제하려면 ctrl+v 후 tab을 누르면 된다.
예시
hello: main.c
g++ -o hello main.c
- 위처럼 짠 이후,
make hello를 하면
main.c가 수정되었는지 확인
target을 지정하지 않을 경우
- target을 지정하지 않고,
make만 수행하면
Makefile의 가장 위의 target을 찾아서 수행
target명과 생성되는 file 이름이 다를 때
- filename으로 build를 해야할지, 말아야할지 판단하므로, 계속 빌드됨.
- 비효율적임
Phony target(유사 타겟)
hello: main.c
g++ -o hello main.c
clean:
rm -rf hello
Makefile을 위처럼 만들면 make clean으로 hello 파일을 지울 수 있다.
- 이렇게 prerequisite없고, 그냥 지정된 명령을 수행하는 것을 Phony target이라 함.
- 그런데
clean이라는 이름의 파일이 존재한다면?
- target명으로 수행여부를 판단하기 때문에,
make clean이 안먹는다.
- 그래서 Phony를 쓰는 거였군!!
.PHONY:clean touch # space로 각자를 구분..
hello: main.c
g++ -o hello main.c
clean:
rm -rf hello
touch:
touch hello
- 요렇게 하면 clean, touch에 대해서 Phony target으로 생각한다.
암묵적 룰
요렇게만 넣어도 자동으로 g++ -c main.c로 만들어준다.
이런 암묵적 룰은
*.c -> *.o*.s -> *.o*.p -> *.o
요런 것들이 존재한다고 한다.
15 Jan 2018
|
tensorflow
eager execution
tensorflow doc 원문
Eager execution
- eager execution을 enable하는 것은 tensorflow 함수들의 동작을 바꾸는 것이다.
- 예를 들면,
Tensor object가 이전에는 computational graph의 노드에 대한 symbolic node였는데
- 그냥 value를 가리키게 된다.
- 결과로, enable은 프로그램 처음 시작시에 해야하며, 중간에 disable은 불가능하다.
import tensorflow as tf
import tensorflow.contrib.eager as tfe
tfe.enable_eager_execution()
위의 코드로 enable을 한다.
x = tf.matmul([[1,2],
[3,4]],
[[4,5],
[6,7]])
y = tf.add(x, 1)
z = tf.random_uniform([5, 3])
print(x)
print(y)
print(z)
tf.Tensor(
[[16 19]
[36 43]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[17 20]
[37 44]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[ 0.8922441 0.6574986 0.13251901]
[ 0.52682853 0.73264265 0.95296896]
[ 0.5486275 0.70670152 0.87073851]
[ 0.43007874 0.50991511 0.6052494 ]
[ 0.15779459 0.66595078 0.8245461 ]], shape=(5, 3), dtype=float32)
NumPy array로 왔다갔다…
NumPy array와 Tensor는 자동으로 호환된다.
- tensorflow의 operation에 numpy array가 들어오면
Tensor로 바뀜
- numpy operation에
Tensor가 들어와도 numpy array로 바뀜
import numpy as np
x = tf.add(1, 1) # tf.Tensor with a value of 2
y = tf.add(np.array(1), np.array(1)) # tf.Tensor with a value of 2
z = np.multiply(x, y) # numpy.int64 with a value of 4
- 사용자가
Tensor object로부터 직접 numpy array를 얻고싶으면 numpy()함수를 호출하면 된다.
print(y)
print(y.numpy())
tf.Tensor(2, shape=(), dtype=int64)
2
GPU acceleration
- Eager execution을 하면 노드를 GPU에 수동할당해야함!
with tf.device('/gpu:0')로 하면 된다.tfe.num_gpus()로 gpu 갯수를 알 수 있다.
x = tf.random_normal([10, 10])
x_gpu0 = x.gpu()
x_cpu = x.cpu()
_ = tf.matmul(x_cpu, x_cpu) # Runs on CPU
_ = tf.matmul(x_gpu0, x_gpu0) # Runs on GPU:0
if tfe.num_gpus() > 1:
x_gpu1 = x.gpu(1)
_ = tf.matmul(x_gpu1, x_gpu1) # Runs on GPU:1
Automatic Differentiation
tfe.gradients_function(f): python 함수 f에 대해서 derivative들을 리턴한다. 물론 f의 인자들에 대해서 미분한다.
- 제약조건:
f는 scalar를 return해야한다.
- return:
Tensor object들의 list
tfe.value_and_gradients_function(f): 위의 함수와 비슷하나, f의 value도 같이 return한다.
인자 하나짜리로 실험을 해보자!
def f(x):
return x*x
df = tfe.gradients_function(f)
print(df(3)) # df 함수의 결과값
print(type(df(3))) # df 함수의 결과값의 type
print(len(df(3))) # df 함수의 결과값의 길이
print(df(3)[0].numpy()) # numpy 값
[<tf.Tensor: id=108, shape=(), dtype=int32, numpy=6>]
<class 'list'>
1
6
'''
3개짜리 인자로 order가 지켜지는지 보자
'''
def f2(x, y, z):
return x*y*z
df2 = tfe.gradients_function(f2)
print(df2(3 ,4, 5)) # order는 지켜지는 것 같다..
[<tf.Tensor: id=149, shape=(), dtype=int32, numpy=20>, <tf.Tensor: id=150, shape=(), dtype=int32, numpy=15>, <tf.Tensor: id=148, shape=(), dtype=int32, numpy=12>]
요 함수들로 model을 학습시키는데 쓸 수 있다. linear regression model을 예로 들어보자
def prediction(input_, weight, bias):
return input_*weight + bias
# toy dataset
num_ex = 1000
training_inputs = tf.random_normal([num_ex])
noise = tf.random_normal([num_ex])
training_outputs = training_inputs * 3 + 2 + noise
def loss(weight, bias):
error = prediction(training_inputs, weight, bias) - training_outputs
return tf.reduce_mean(tf.square(error))
grad = tfe.gradients_function(loss)
W = 5.
B = 10.
lr = 0.01
print("initial loss: {}".format(loss(W, B).numpy()))
for i in range(200):
(dW, dB) = grad(W, B) # 이러면 귀찮아지는데....
W -= dW * lr
B -= dB * lr
if i % 20 == 0:
print("loss at step {}: {}".format(i, loss(W,B).numpy()))
print("final loss: {}".format(loss(W,B).numpy()))
print("W:{}, B:{}".format(W.numpy(), B.numpy()))
initial loss: 69.62956237792969
loss at step 0: 66.85037231445312
loss at step 20: 29.827312469482422
loss at step 40: 13.637370109558105
loss at step 60: 6.5486159324646
loss at step 80: 3.4408247470855713
loss at step 100: 2.0765790939331055
loss at step 120: 1.476935863494873
loss at step 140: 1.213025689125061
loss at step 160: 1.0967267751693726
loss at step 180: 1.045410394668579
final loss: 1.0234872102737427
W:3.024306297302246, B:2.182044744491577
custom gradient
함수가 어떤 지점에서 numerical instability를 가진다면 다음과 같이 gradient를 커스터마이즈해서 쓸 수 있다.
@tfe.custom_gradient
def log1pexp(x):
e = tf.exp(x)
def grad(dy):
return dy * (1 - 1 / (1 + e)) # 위에서 계산한 e를 갖다썼는데, 이게 계산량을 줄여준다
return tf.log(1 + e), grad
grad_log1pexp = tfe.gradients_function(log1pexp)
model 만들고 학습하기
아까 prediction을 보면 loss에 gradient를 구하고, 거기에 인자로 parameter들을 넣고 최적화함.
실제로 모델을 만들어서 최적화하려면 파라미터도 엄청 많을 것이다. 이대로는 못쓴다.
Variables and Optimizers
tfe.implicit_gradients
f에 쓰인 모든 인자의 derivatives를 계산- 반환된 함수를 호출하면, (grad val, Variable object) 튜플의 리스트를 반환
class Model(object):
def __init__(self):
self.W = tfe.Variable(5., name='weight')
self.B = tfe.Variable(10., name='bias')
def predict(self, inputs):
return inputs * self.W + self.B
# The loss function to be optimized
def loss(model, inputs, targets):
error = model.predict(inputs) - targets
return tf.reduce_mean(tf.square(error))
# A toy dataset of points around 3 * x + 2
NUM_EXAMPLES = 1000
training_inputs = tf.random_normal([NUM_EXAMPLES])
noise = tf.random_normal([NUM_EXAMPLES])
training_outputs = training_inputs * 3 + 2 + noise
# Define:
# 1. A model
# 2. Derivatives of a loss function with respect to model parameters
# 3. A strategy for updating the variables based on the derivatives
model = Model()
grad = tfe.implicit_gradients(loss)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
# The training loop
print("Initial loss: %f" %
loss(model, training_inputs, training_outputs).numpy())
for i in range(201):
optimizer.apply_gradients(grad(model, training_inputs, training_outputs))
if i % 20 == 0:
print("Loss at step %d: %f" %
(i, loss(model, training_inputs, training_outputs).numpy()))
print("Final loss: %f" % loss(model, training_inputs, training_outputs).numpy())
print("W, B = %s, %s" % (model.W.numpy(), model.B.numpy()))
Initial loss: 68.121872
Loss at step 0: 65.497581
Loss at step 20: 30.059015
Loss at step 40: 14.102830
Loss at step 60: 6.915086
Loss at step 80: 3.675683
Loss at step 100: 2.215032
Loss at step 120: 1.556112
Loss at step 140: 1.258721
Loss at step 160: 1.124437
Loss at step 180: 1.063774
Loss at step 200: 1.036357
Final loss: 1.036357
W, B = 3.00555, 2.15338
10 Jan 2018
|
ml
generative model
원본
서론
이 페이퍼는 generative model의 배경설명부터 시작한다.
- generative model을 학습시킬 때, data가 어떤 Unknown distribution $P_r$에서 부터 온다고 가정한다.(r은 real을 뜻함)
- 그리고 우리는 그 $P_r$을 근사시키는 $P_\theta$를 학습시키고 싶어한다.(여기서 $\theta$는 parameter)
- 이제, 이를 만족시키는 두가지 방법을 찾을 수 있는데,
- $P_\theta$를 직접 학습시킨다: MLE를 통해 $P_\theta$를 학습
- 어떤 다루기 쉬운 distribution $Z$에서 $P_\theta$로 가는 transform function을 학습한다.
- 보통 이때 $Z$는 Gaussian dist를 쓴다.
- $P_\theta = g_\theta(Z)$
- 이제 처음 방법의 문제를 설명해보자.
- $P_\theta$가 주어졌을 때, MLE objective는
-
- 그리고 이는 m을 무한대로 보내면 KLD와 같다
- $P(x) \ge 0$인 어떤 x에서 $Q(x) = 0$이면 KLD가 무한대로 감
- This is bad for the MLE if $P_\theta$ has low dimensional support, because it’ll be very unlikely that all of $P_r$ lies within that support.(뭔말인지…wiki를 보면 0이아닌 domain의 subset을 말하는 것 같다.)
- 아니면 학습 시, random noise를 주는 방법도 존재!
- distribution이 어디서는 정의되어있다는 것을 보장해주나, 학습시에 random noise를 뿌리는건 별로다.(정말?)
- 그래서 두번째 방법으로 구현을 하게된다.
- 두번째 방법
- inference 방법
- $z \sim Z$ sample
- $g_\theta(Z)$로 evaluation
- $g_\theta$를 학습시키기 위해 distribution들의 거리를 재는 measure가 필요하다.
여러 Distance들
- total variation(TV)
- $\delta(P_r, P_g) = \sup_{A} \vert P_r(A) - P_g(A) \vert$
- 두 dist에서 벌어질 수 있는 값중 가장 큰 값
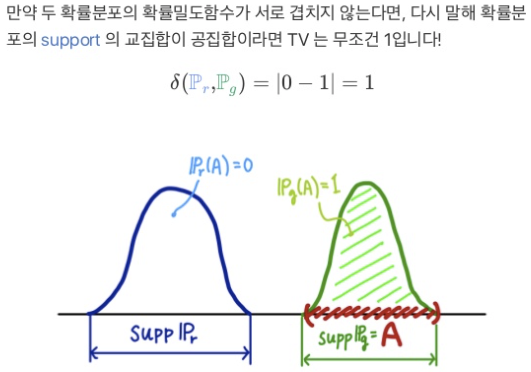 참고…
참고…
- KL-divergence(KLD)
- $KL(P_r|P_g) = \int_x \log\left(\frac{P_r(x)}{P_g(x)}\right) P_r(x) \,dx$
- Jenson-shannon-divergence(JSD)
- $JS(P_r,P_g) = \frac{1}{2}KL(P_r|P_m)+\frac{1}{2}KL(P_g|P_m)$
- W-distance(EM-dist)
- $W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[||x - y||\big]$
- 여기를 보자 BEGAN
Next: 근데, 이 녀석들을 보니까 W-distance 빼고는 전부 너무 hard한 녀석들! (distribution이 겹치지 않으면 불연속이 된다.)
그래서 W-distance를 쓴다.
example
다음과 같은 distribution을 보자. $R^2$에 대해서 정의되어있으며, 실제 distribution은 $(0,y)$인데, $y \sim U[0,1]$이라 하며, $P_\theta=(\theta, y)$라 하자.
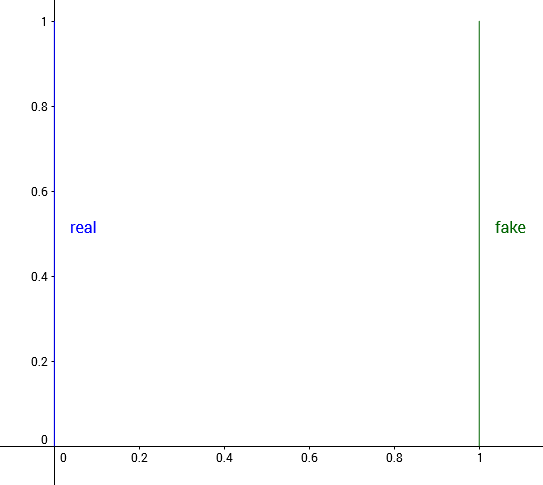 이제 우리가 하고픈 일은 $\theta \rightarrow 0$으로 이동시켜서 distance를 줄어들게하는 것이다.
이제 우리가 하고픈 일은 $\theta \rightarrow 0$으로 이동시켜서 distance를 줄어들게하는 것이다.
그래서 W-gan에서는 EMD를 써서 학습을 잘 시키도록 했다는 말..
Wasserstein GAN
- 근데 사실 W-distance가 intractable하다.
- $W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[||x - y||\big]$
- 그래서 이를 근사시켜서 푼다
-
- f가 1-lipshcitz 함수여야함 (기울기가 1을 넘지 않는 함수)
- 근데 이를 K-lipshcitz 함수로 바꿔도 문제가 안생긴다고 함…
- 대충 그러면
- $\theta$를 고정시키고 $f_w$를 수렴시킨다
- 구한 $f_w$와 새로 샘플링한 $z$로 $-E_{z \sim Z}[\nabla_\theta f_w(g_\theta(z))]$를 구하고 gradient를 구한다
- $\theta$ update
알고리즘






 사진 출처
사진 출처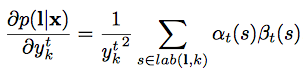
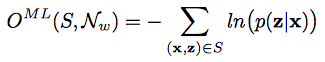
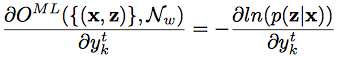
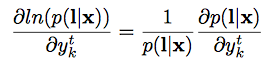
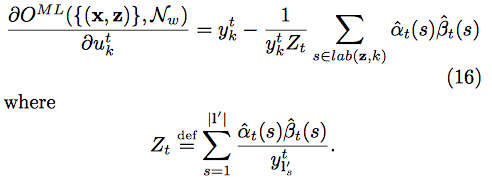




 이제 우리가 하고픈 일은 $\theta \rightarrow 0$으로 이동시켜서 distance를 줄어들게하는 것이다.
이제 우리가 하고픈 일은 $\theta \rightarrow 0$으로 이동시켜서 distance를 줄어들게하는 것이다.