ubuntu에 mysql 설치
20 Dec 2017 | mysql utf8mysql 설치
기본 설치
sudo apt-get update
sudo apt-get install mysql-server
mysql_secure_installation
이후 적당히 봐가면서 y/n 해주자..
mysql 중지 및 db 경로 이전
여기서는 /data2/mysql/로 db 경로를 이전한다고 가정한다.
db 데이터 복사
sudo service mysql stop
sudo rsync -av /var/lib/mysql /data2/
sudo chown -R mysql:mysql /data2/mysql
datadir 경로 수정
sudo vi /etc/mysql/mysql.conf.d/mysqld.cnf로 열고 다음으로 수정한다.
datadir = /data2/mysql
apparmor 설정
잘 모르는 내용이라 검색해봤는데, 우분투에서 앱의 resource 접근 제한등을 컨트롤하는 것이라 한다참고.
sudo vi /etc/apparmor.d/usr.sbin.mysqld 에서 다음 경로를 수정하자(/var/lib/mysql로 되어있었던 부분을… )
# Allow data dir access
/data2/mysql/ r,
/data2/mysql/** rwk,
sudo vi /etc/apparmor.d/abstractions/mysql에서 또 첫 줄의 /var/lib/mysql{,d}/mysql{,d}.sock rw,를
/data2/mysql{,d}/mysql{,d}.sock rw,
로 바꿔주면 된다.
이제 마지막으로 apparmor를 재시작 후, mysql을 다시 시작
sudo /etc/init.d/apparmor reload
sudo service mysql start
동작 확인
mysql에서 현재 datadir을 보는 방법은 다음과 같다.
select @@datadir;
제대로 나오면 성공!
mysql 캐릭터셋 변경
역시 mysql service를 내리고 작업한다.(sudo service mysql stop)
/etc/mysql/mysql.conf.d/mysqld.cnf에서
[client]
default-character-set = utf8
[mysqld]
skip-character-set-client-handshake
character-set-server = utf8
collation-server = utf8_general_ci
init-connect = SET NAMES utf8
/etc/mysql/conf.d/mysql.cnf에서
[mysql]
default-character-set = utf8
/etc/mysql/conf.d/mysqldump.cnf에서
[mysqldump]
quick
quote-names
max_allowed_packet = 16M
default-character-set = utf8
이제 다시 mysql을 키고 확인한다. (sudo service mysql start)
show variables like 'char%';로 확인했을 때,
+--------------------------+----------------------------+
| Variable_name | Value |
+--------------------------+----------------------------+
| character_set_client | utf8 |
| character_set_connection | utf8 |
| character_set_database | utf8 |
| character_set_filesystem | binary |
| character_set_results | utf8 |
| character_set_server | utf8 |
| character_set_system | utf8 |
| character_sets_dir | /usr/share/mysql/charsets/ |
+--------------------------+----------------------------+
8 rows in set (0.00 sec)
요렇게 나오면 성공!
마지막 삽질기 (제대로 덤프가 안될 때)
mysqldump로 dump를 하면, utf8 데이터가 제대로 덤프가 안되는 경우가 있다. 이때 latin1으로 dump를 뜬 후 mysqldump -u eval -p EVAL –default-character-set=latin1 > 20171219.sql 해당 파일의 latin1을 utf8로 바꿔치고 데이터를 넣으면 된다….;;
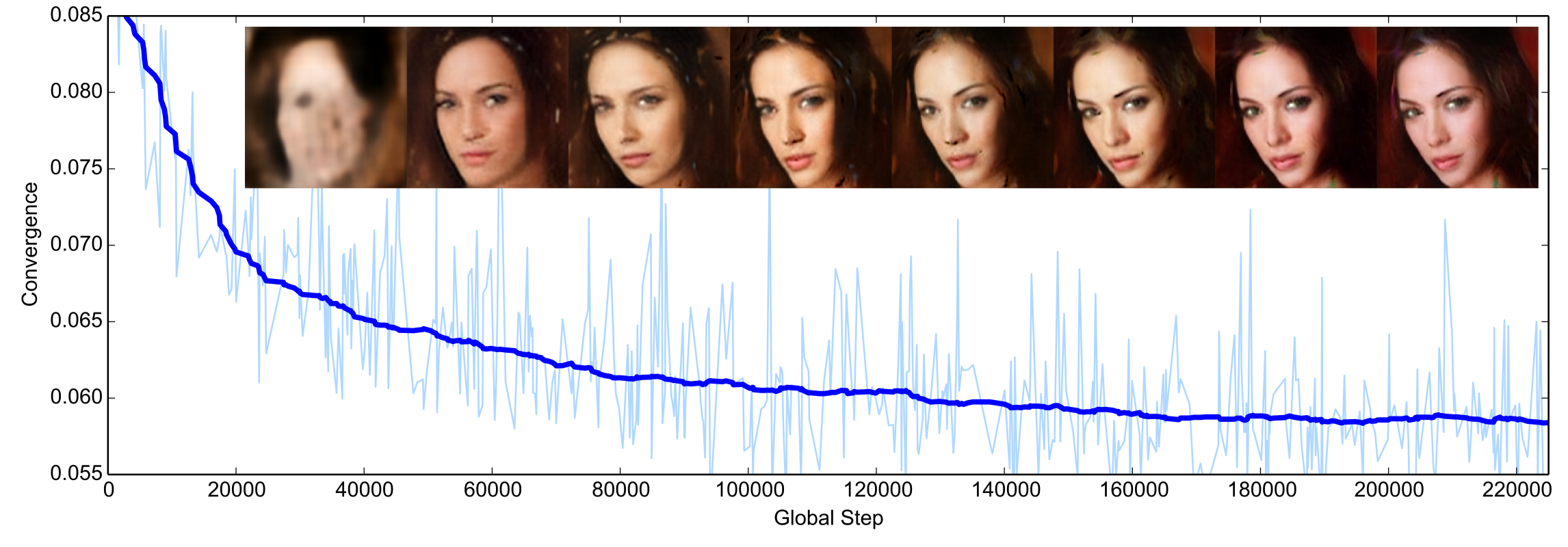
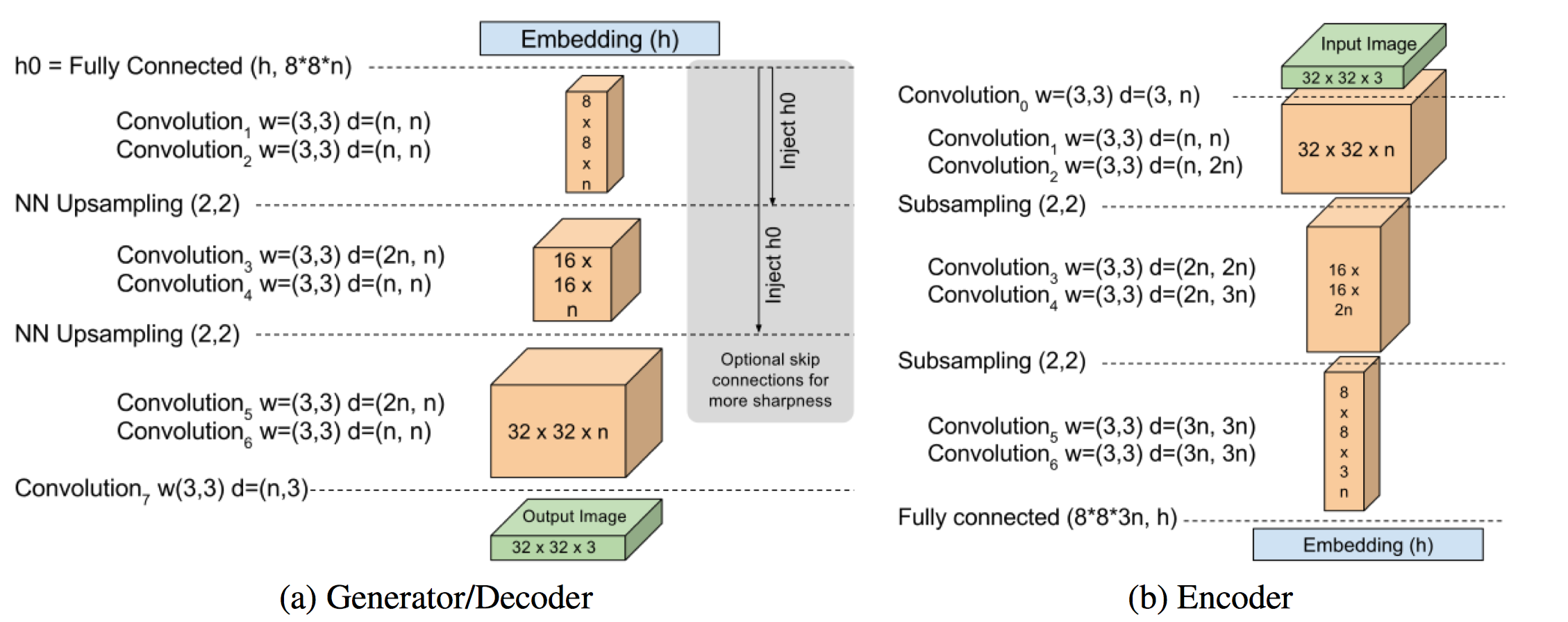
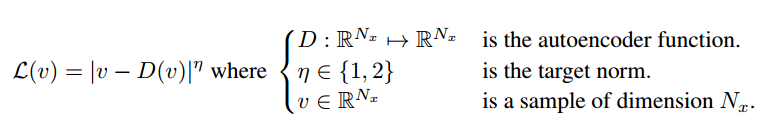그냥 단순히 AE를 거친 input과 output의 pixel별 로스를 구해서 l-1,l-2 norm중에 하나를 취한다.
